
我最喜歡的一些空間:拓撲學家的正弦曲線
拓撲學家的正弦曲線是連通但不路徑連通的空間的經典例子:你可以看到終點線,但你無法從這裡到達那裡。
艾芙琳·蘭姆是一位居住在猶他州鹽湖城的自由數學和科學作家。

我最喜歡的一些空間:拓撲學家的正弦曲線
拓撲學家的正弦曲線是連通但不路徑連通的空間的經典例子:你可以看到終點線,但你無法從這裡到達那裡。

證明、布丁和π:讓你感到飢餓的數學書
需要一些夏季讀物嗎?程 Eugenia 的《如何烘焙 Pi》和 Jim Henle 的《證明和布丁》向我們展示了數學和烹飪之間的共同點比你想象的要多。
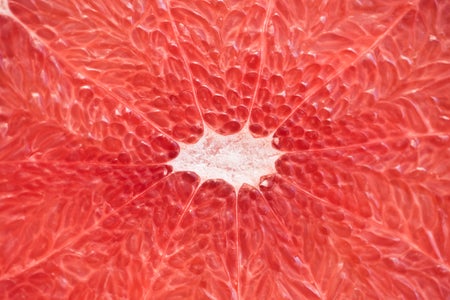
葡萄柚數學
球面幾何:它是這份完整早餐的一部分。

我最喜歡的一些空間:胖康託集
上個月,我寫了關於康託集的文章,康託集是一個有趣的數學空間,它混合了小和大。從某種意義上說,它是小的,因為它的長度是 0。

數學,現場直播:與 Katie Steckles 和 Laura Taalman 的對話
兩位數學傳播者談論他們如何對數學產生興趣以及如何與他人分享他們的熱情

讚美分形和詩歌
在數學詩歌月,一首關於分形的詩

蘭伯特論幾何中的愛與恨
雙曲幾何的歷史充滿了雙曲的引言,我在本學期早些時候的數學史課上偶然發現了一句優美的引言。

康託函式:天使還是魔鬼?
當你看著它時,它只是停在那裡,恆定而靜止。但是,如果你在康託集中的某個點瞬間轉過身,函式就會以令人難以置信的速度增長。

我最喜歡的一些空間:康託集
康託集很大,但那裡並沒有太多東西。

連分數有什麼了不起的?
連分數在逼近技術方面客觀上是最好的

不要背誦數字來慶祝 Pi。而是背誦它的連分數。
當你慶祝這個超越數時,超越小數

優步,但用於拓撲空間
所以現在又冷又下雨,你熬夜到很晚,試圖弄清楚為什麼定理中需要那個討厭的假設。如果你可以訂購一個路徑連通但不區域性連通的空間,那豈不是很好嗎?

在第四維度中製作和做的事情(書評)
有時你想從一本通俗數學書中學習一種“新的”乘法演算法,有時你想了解為什麼投票系統註定是不完美的,有時你只是想玩弄數字、模式和圖片。

媒體和天才神話
我們不應該讓對“天才”數學家的描繪將我們其他人拒之數學門外。

用這個奇怪的數字瞭解麻疹爆發
基本傳染數以及它為什麼重要

學習像埃及人一樣計數
上學期,我開始我的數學史課程時講了一些巴比倫算術。我們所做的數學很簡單——乘法和加法、透過配方法求解二次方程——但是 60 進位制和缺少真正的零使得這些基本運算對我的學生來說具有挑戰性。

數學,現場直播:與 Amal Fahad 和 Rasha Osman 的對話,第二部分
我很高興參加了九月份舉行的第二屆年度海德堡桂冠論壇。它以林道諾貝爾獎獲得者會議為藍本,彙集了數學和計算機科學領域著名獎項的獲得者以及這些領域的青年研究人員。

數學,現場直播:與 Amal Fahad 和 Rasha Osman 的對話,第一部分
我很高興參加了九月份舉行的第二屆年度海德堡桂冠論壇。它以林道諾貝爾獎獲得者會議為藍本,彙集了數學和計算機科學領域著名獎項的獲得者以及這些領域的青年研究人員。

今年我寫得太開心的 12 件事
現在是家人、熱巧克力和年度回顧清單的季節。猜猜這是哪一個!“單位根”已經存在兩年了,我很高興我有一個地方可以分享我思考的一些奇怪而奇妙的數學。

當我們談論孔洞時,我們在談論什麼
在萬聖節,我寫了一個非常可怕的話題:高階同倫群。同倫是拓撲學中的一個概念,拓撲學是數學的一個分支,它關注形狀的屬性,無論你如何擠壓或拉伸它們,這些屬性都保持不變,只要你不撕裂它們或將東西粘在一起。

線上遊戲眾包定理
現在是你證明一些定理的機會,而無需知道它們的含義!費爾菲爾德大學的數學家克里斯·斯泰克建立了遊戲“好鄰居”,以獲得來自數字拓撲領域的眾包問題解決方案。

看見音樂:缺失的基頻是什麼樣的?
我昨天寫了一篇關於缺失基頻效應的文章。這是一種令人吃驚的聽覺錯覺,你的大腦會聽到一個比任何實際播放的音符都低的音符。

你的電話在聲音方面對你撒謊
電話在聲音方面撒謊是因為奇數不是偶數。再次與那些整數和聲音感知有關!電話只能接收到 300 或 400 赫茲以上的頻率(每秒週期,也稱為 Hz),但大多數成年人的說話聲音都低於 300 赫茲(大約是中央 C 上方的 D 音)。

我所知道的關於整數的最悲哀的事情
我們無法調音鋼琴,因為素數