
你能區分數學和詩歌嗎?參加測驗找出答案
“_______是邏輯思想的______”—阿爾伯特·愛因斯坦。 “數學”或“詩歌”這兩個詞填空哪個更合適?
伊芙琳·蘭姆是一位居住在猶他州鹽湖城的自由數學和科學作家。

你能區分數學和詩歌嗎?參加測驗找出答案
“_______是邏輯思想的______”—阿爾伯特·愛因斯坦。 “數學”或“詩歌”這兩個詞填空哪個更合適?

我最喜歡的空間之幾:圓環面
數學總是與可定向的虧格為 1 的糕點搭配更佳,這是最美味的拓撲學例子。

跑步中的數學
如果你以每公里 3:07 的平均速度跑完一場比賽,你是否在任何一公里都正好跑了 3:07?嗯,這很複雜。

解開變形空間的奧秘,數學家贏得 300 萬美元獎金
第二屆年度數學突破獎授予加州大學伯克利分校的拓撲學家伊恩·阿戈爾
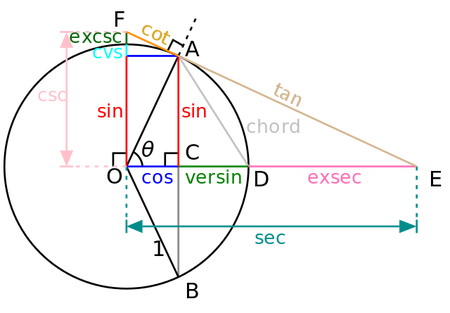
我寫過的最可怕的數學故事
讀完這些後,你可能需要在晚上開著燈睡覺。準備好迎接殭屍、惡魔、木乃伊和……更高階的同倫群了嗎?

爭議教學:5 × 3 是五個 3 還是三個 5?
最新的(被誤稱的)“共同核心數學”爭議:5 × 3 是五個 3 還是三個 5?
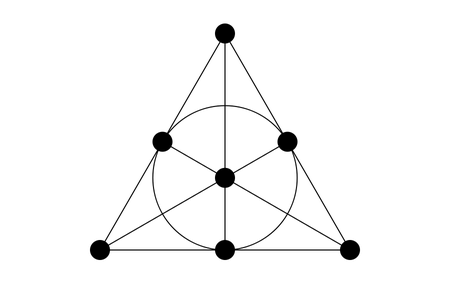
我最喜歡的空間之幾:法諾平面
挑戰直覺的法諾平面可能是點和線最小的有趣配置。

ε 和 δ 的詭計
ε-δ 證明是許多微積分學生的剋星,是進入證明寫作奧秘的入門儀式。

一次一刀,製作你自己的字型
四色定理靠邊站!現在是單刀定理的時間了:如果你願意進行一些巧妙的摺疊,你可以用一刀剪出任何你想要的形狀
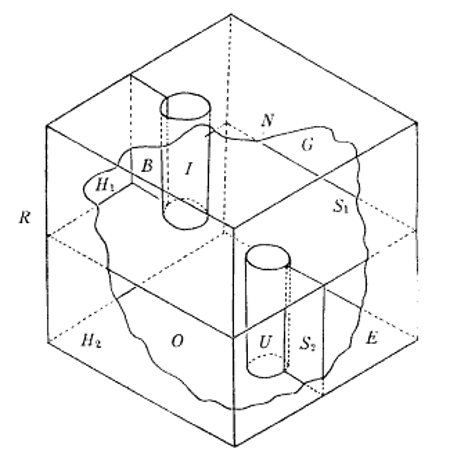
我最喜歡的空間之幾:雙室房屋
理解一個數學物件意味著什麼?在我為自己建造雙室房屋之前,我並沒有真正相信它的存在。

不可能的桌布和神秘曲線:探索數學和藝術中的對稱性
在他的新書《創造對稱性》中,弗蘭克·法里斯運用高等數學的思想,如複分析和抽象代數,將風景、鮮花,甚至他的晚餐快照轉化為美麗的重複設計。
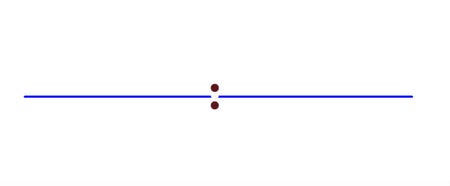
我最喜歡的空間之幾:具有兩個原點的直線
這條可證明不可繪製的具有兩個原點的直線說明了一個簡單但重要的拓撲性質

改變你的開集,改變你的人生
開集的概念是拓撲學的基礎。它是什麼,為什麼它很重要?

在 8,812 孔甜甜圈上的史詩般的探索
大衛·馬多爾的線上迷宮讓你可以在你最喜歡的網路瀏覽器的舒適環境中探索複雜的雙曲曲面。

在雙曲平面中一切看起來都更好
將你自己或你最喜歡的數學家變成雙曲平面的平鋪藝術品。
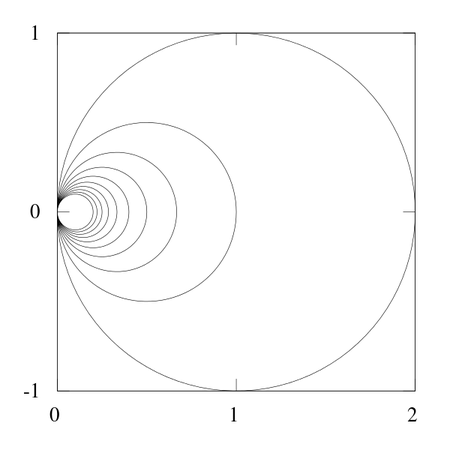
我最喜歡的空間之幾:無限耳環
拓撲學是關於擠壓和拉伸的;距離應該無關緊要。但是無限耳環說明了拓撲學和幾何學之間微妙的相互作用。
在 Bridges 與我一起製作數學音樂
加入我在巴爾的摩 Bridges 數學+藝術會議上的數學、音律和音高感知研討會。

世界上最準確的鑲木地板性格測試
你是神經質的孤獨者還是有魅力的邪教領袖?試試這個高度科學的性格測試,它基於安東尼·高迪的現代主義傑作之一的鑲木地板來找出答案

成為塞德里克·維拉尼是什麼感覺
菲爾茲獎章獲得者的回憶錄讓我們得以一窺成為一位充滿熱情的數學家的情感高潮和低谷。

幫助讓可穿戴蜂窩自動機成為現實
法比安·塞裡耶想要破解一臺工業針織機來製作蜂窩自動機圍巾,你可以在 Kickstarter 上支援她的專案。

作為數學家難以忍受的字面主義
數學家,就像盜竊癖患者一樣,會字面意思地理解事物。這是一個關於我如何最終爆發並寫了一篇措辭強烈的博文,解釋了為什麼文學免責宣告讓我惱火的故事。

對莫扎特和模算術的遲來的道歉
莫扎特和模算術有什麼共同之處?我曾經認為我不喜歡它們。對不起,莫扎特和模算術。請原諒我。
我最喜歡的空間之幾:康託的漏帳篷
稱為康託的漏帳篷的數學空間是連通的,但僅僅是勉強連通:移除一個點,整個結構就會瓦解。

當《蒙娜麗莎》是 NP 困難問題時
鮑勃·博世和湯姆·韋克斯勒開發了一種新方法,可以將你最喜歡的傑作變成連點成線謎題。你只需要一點量化和大量的計算時間。