亨利·歐內斯特·杜德尼可能是最偉大的謎題發明家之一。他於 1857 年出生於英格蘭的梅菲爾德,是一位鄉村教師的兒子,於 1930 年去世。杜德尼數十年來定期為報紙和雜誌設計腦筋急轉彎,後來他將大部分謎題編纂成書。這個難題出自他 1917 年出版的《數學趣題》一書。
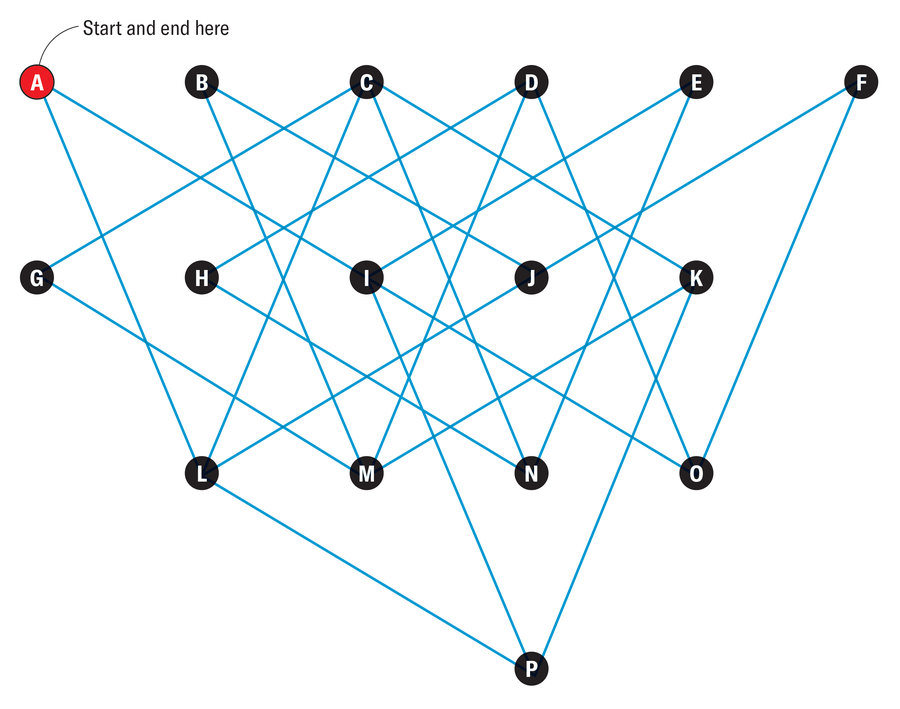
一位住在 A 城市的旅行推銷員想在一週內訪問從 B 到 P 的所有城市,但不一定按字母順序排列,並在最後返回 A 城市。他計劃每個城市只進入一次。藍線是連線這 16 個城市的唯一道路。這位旅行推銷員只能使用任何兩個城市之間的直線路線;他不得在兩條街道的交叉口轉彎。有多少種不同的路線是可能的?
答案
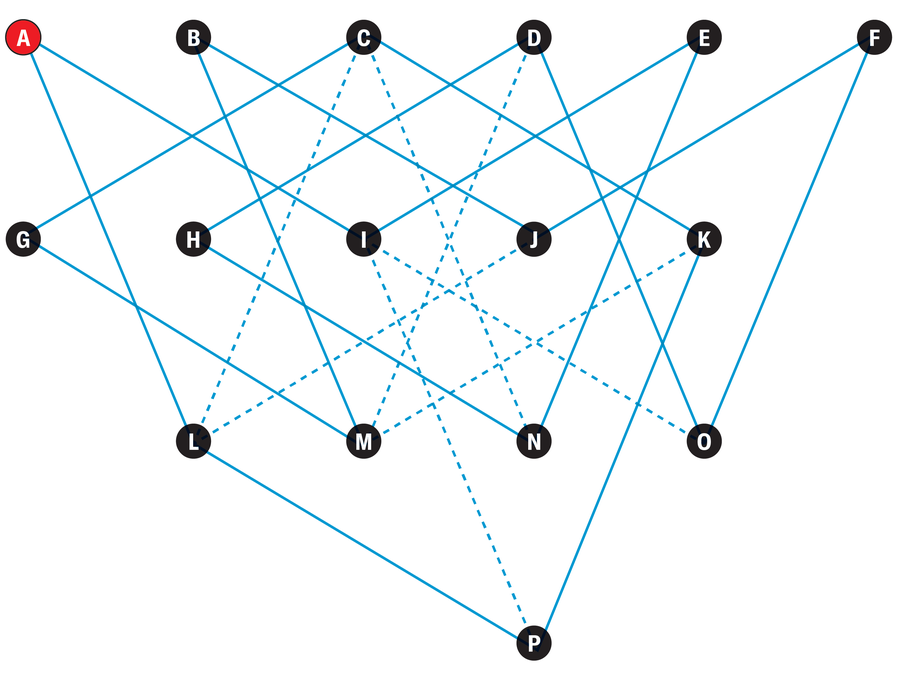
如果這位旅行推銷員透過一條路進入一個城市,他必須透過另一條路離開。為了使往返行程成為可能,至少必須有兩條道路通往每個城市。恰好有兩條道路通往城市 A、B、E、F、G 和 H。因此,無論如何,這位旅行推銷員都必須走這些路。這也決定了他將使用哪些道路到達和離開城市 I、J、M 和 N。剩餘的連線也很清楚。因此,這位旅行推銷員只有一種可能的往返行程——AIENHDOFJBMGCKPLA——但他可以沿兩個不同的方向行駛。
我們很樂意聽到您的來信!請傳送電子郵件至 games@sciam.com 分享您的體驗。
這個謎題最初出現在《Spektrum der Wissenschaft》雜誌上,並已獲得許可轉載。