本文發表於《大眾科學》的前部落格網路,僅反映作者的觀點,不一定代表《大眾科學》的觀點
艾倫·圖靈在《形態發生的化學基礎》中提出,化學物質(形態素)可以轉化並在組織中擴散,從而產生在動物身上看到的自然圖案——條紋、斑點和螺旋。圖靈用微分方程的語言表達了這個想法,微分方程的初始條件控制著圖案的演變。
這種反應-擴散系統產生的圖案的複雜性和細節可能非常令人驚訝——一個相對簡單的過程和少量的引數可以產生無窮無盡的熟悉圖案和形狀。一個應季的例子是雪花,以其多樣性和複雜性而聞名。
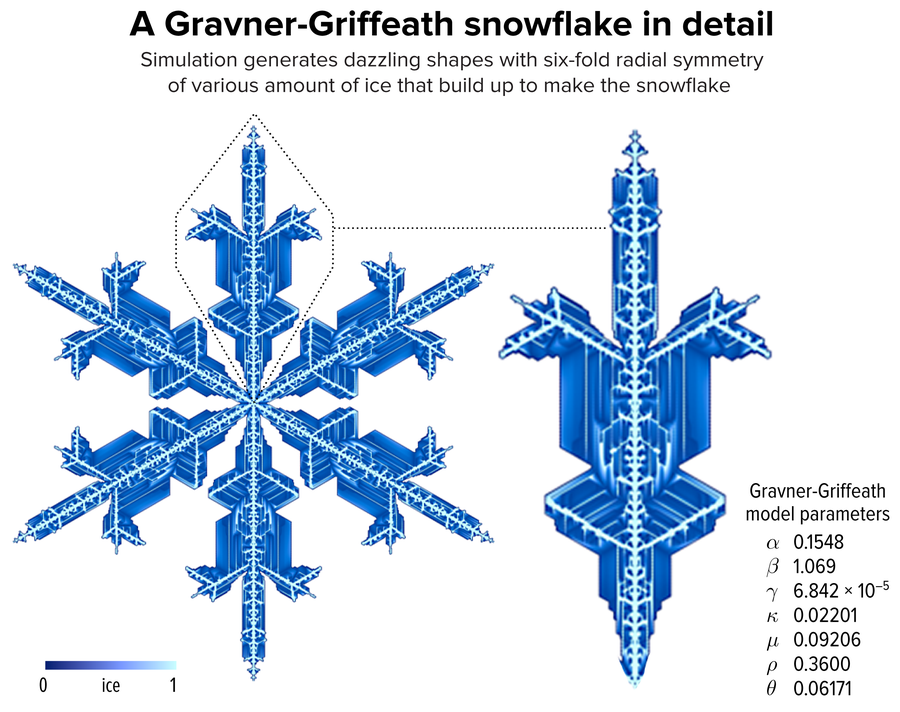
圖 1. 使用 Gravner-Griffeath 模型生長的雪花示例。雪花不同部位的不同冰量(用藍色調編碼)構成了六重徑向對稱形狀。您可以在我們的線上雪花收藏中瀏覽有關此雪花的詳細資訊。致謝:Martin Krzywinski 和 Jake Lever
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和思想的具有影響力的故事。
使用 Gravner-Griffeath 模型可以模擬出令人信服的逼真雪花,您可以使用作者提供的程式碼自行執行(圖 2)。雪花的徑向對稱性繼承自它生長的六邊形網格。在不同的網格站點模擬了三種不同型別的質量:冰、準液體和蒸汽。最初,在雪花站點初始化 ρ 量的冰,並在其他所有地方初始化 ρ 蒸汽質量。然後,該模型透過擴散、凍結(由 κ 控制)和融化(由 μ 和 γ 控制)來傳輸和轉換這些質量的一部分。例如,在凍結過程中,邊界質量處一部分 κ 的蒸汽變成冰,剩餘部分 1–κ 變成準液體。雪花周圍的邊界站點透過附著過程成為雪花的一部分,該過程由引數 α、β 和 θ 控制,這些引數充當截止值。一旦一個站點成為雪花的一部分,它的所有質量都變成不再變化的冰。

圖 2. Gravner-Griffeath 模型是一種反應-擴散系統,具有三種“形態素”:冰、準液體和蒸汽。該模型是確定性的——給定一組引數,輸出始終相同。可選地,該模型可以透過在每個步驟擾動每個站點中的蒸汽質量量來包含隨機性。致謝:Martin Krzywinski 和 Jake Lever
我們所有的雪花都在 800 × 800 的六邊形網格上生長,最多 30,000 個生長步驟,並在此處以矩形網格呈現,透過旋轉和縮放獲得。雪花始終以網格中心的單個站點初始化,當它們生長到接近網格邊界時,被認為已完全長大,此時模擬結束。在圖 3 中,我們跟蹤了圖 1 中雪花的生長過程。選擇顏色圖是為了在淺色背景上繪製時突出雪花的邊界——請注意,淺藍色代表高質量,而深藍色代表低質量。

圖 3. 雪花從圖 1 到完全長大(15,353 個生長步驟)的演變過程。致謝:Martin Krzywinski 和 Jake Lever
圖 1 中的雪花用了 15,353 步才完全長大。在圖 3 的第一行影像中可以看到生長速度。在第二行中,每張影像都被放大不同的量,以更好地揭示較小雪花生長過程的細節。請記住,一旦一個站點加入雪花,其質量在模擬期間是固定的。最初,冰質量沿著對稱軸累積,並迅速開始出現微小的凸起。這些凸起長成樹枝,因為蒸汽不必像到達雪花其他部分那樣擴散那麼遠才能到達凸起。這個過程稱為分支不穩定性,併產生樹枝狀雪花。
雪花在內角處生長迅速,因為對於擁有超過 3 個雪花鄰居的邊界站點,附著過程是自動的。這使得沉積物具有少量質量(深藍色)來填充雪花。這稱為刻面,它與分支相反。刻面雪花具有簡單的平坦表面。到 2,000 次迭代時,我們看到分支減慢,並且出現越來越多的刻面(深藍色)。
蒸汽的作用可以在第三行影像中看到,該影像使用灰度描繪了每個空氣站點中的蒸汽質量量。蒸汽量透過凍結 (κ)、融化 (γ) 以及附著影響冰的形成,其中如果其鄰域中的蒸汽量小於 θ 且準液體量高於 α,則具有三個雪花鄰居的邊界單元可以附著。

圖 4. 改變每個模型引數對圖 1 中雪花形狀的影響,其引數值顯示為紅點。影像對小黑刻度線顯示的引數值進行取樣。我們的雪花集合中按引數值分佈的情況顯示為灰色直方圖。中位數是箱子之間的長黑線。致謝:Martin Krzywinski 和 Jake Lever
儘管該模型相對簡單,但引數對雪花形狀的影響卻相當複雜。為了瞭解引數如何影響形狀,我們使用圖 1 中的雪花作為對照,並在可行雪花的範圍內系統地改變了它的每個引數。我們所說的“可行”是指那些在 30,000 次迭代後沒有長成微不足道的六邊形並且佔據了六邊形網格 60% 以上的雪花——這類雪花約佔使用隨機生成的引數值生長的雪花的 10%。
例如,增加控制總質量量的 ρ 會提高生長速度並鼓勵分支。我們圖 1 中的雪花 ρ 值較低,因此分支不多。增加 θ 和減少 α 都會鼓勵刻面,因為這些引數是附著的截止值。
鑑於圖 4 中形狀的巨大變化,嘗試根據相似性對雪花進行聚類是合理的。已經有人提出了複雜的雪花分類系統。這些包括扇形板(簡單六邊形,圖 4 中 θ = 0.081)、星狀板(完全星狀雪花,圖 4 中 μ = 0.072)、星狀枝晶(分支雪花,圖 4 中 α = 0.18)和蕨狀星狀枝晶(高度分支,圖 4 中 ρ = 0.5)等類別。有趣的是,透過改變圖 1 中雪花(星狀枝晶)的單個引數,可以用多種方式獲得這些類別中的每一個。
對雪花進行分組有兩種選擇:按引數值或按形狀。最初,我們的計劃是按引數建立分組,我們認為這更接近模型的內部工作原理。然而,如圖 4 所示,引數空間非常混亂——引數的微小變化可能會導致形狀的巨大差異。因此,我們選擇使用形狀,我們希望這將建立更具視覺吸引力的組,我們稍後可以將這些組與引數值相關聯(圖 5)。
由於我們在 800 × 800 的網格上生長雪花,因此每片雪花都可以被視為長度為 640,000 的向量,其中的值是蒸汽或冰質量。具有相似向量(透過歐幾里得距離測量)的雪花具有相似的形狀。但是,對於我們大約 15,000 片雪花的集合,對如此大的向量進行聚類在計算上是不可行的。我們透過將雪花按五分之一的因子進行下采樣來解決這個問題,以建立一個 160 × 160 的網格,我們進一步使用高斯濾波器對其進行模糊處理,以消除相似雪花之間的小差異。任何一對雪花之間的相似性是相應 25,600 元素向量之間的歐幾里得距離。
使用計算出的雪花之間的相似性,我們對它們的“距離”有了一個概念。不幸的是,這個距離是在一個 25,600 維的空間中表示的。為了視覺化這個空間,習慣上將這個空間降維到二維,以便我們可以在頁面上繪製它。
對此的常用方法是主成分分析 (PCA),它識別資料集內最大方差的軸,並旋轉資料,使第一維顯示最大方差。本質上,選擇旋轉是為了儘可能多地保留資料中的趨勢。PCA 假設資料集具有線性,這當然被我們的雪花所違反。然而,PCA 識別出 θ(附著)和 ρ(質量)與前兩個主成分高度相關。這確實按雪花的“豐滿度”對雪花進行了分離,但無法區分較小的分組。
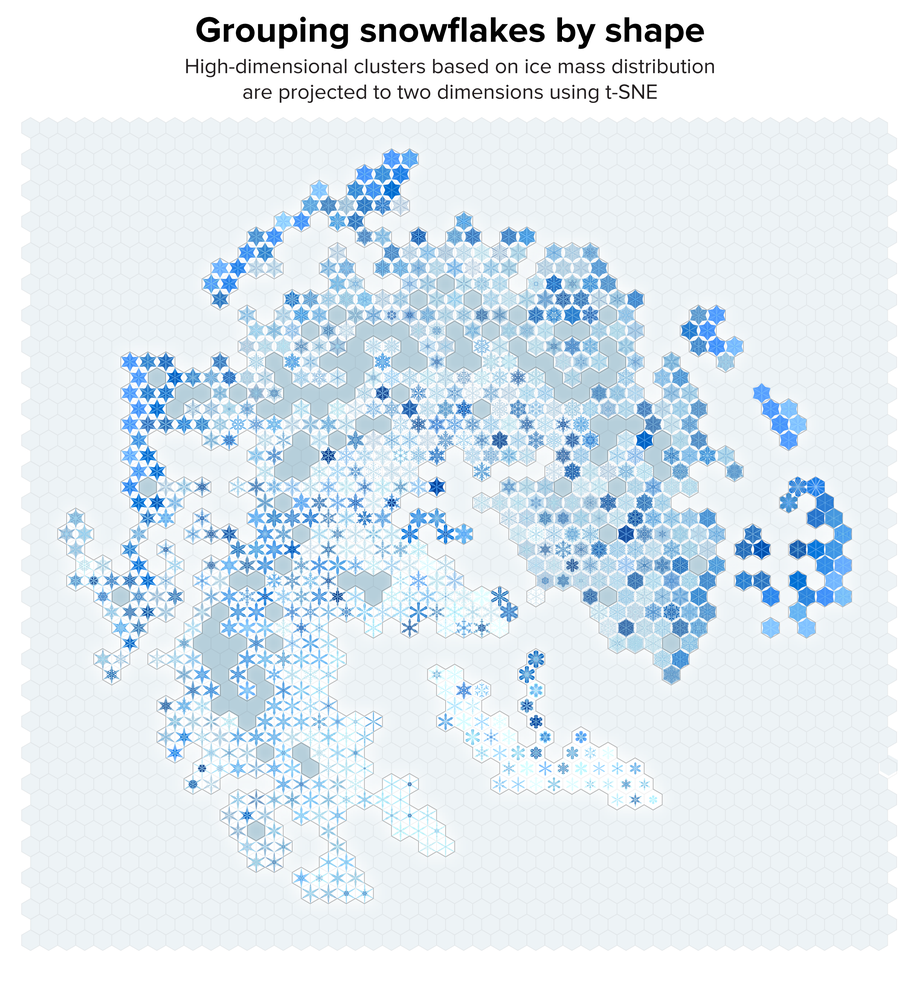
圖 5. 我們基於結構相似性聚類的雪花集合。使用 t-SNE 將聚類投影到二維空間。雪花本身排列在六邊形網格上,以實現更緊密的堆積。致謝:Martin Krzywinski 和 Jake Lever
PCA 的替代方法是 t-分佈隨機鄰域嵌入 (t-SNE)。此方法使用以下原理:高維空間中相似的雪花應放置在低維空間中彼此靠近的位置。它將兩片雪花的相似性建模為高維空間和低維空間中的機率分佈,並最大限度地減少這兩個分佈之間的差異。設 dij 為雪花 i 和 j 之間的歐幾里得距離,則
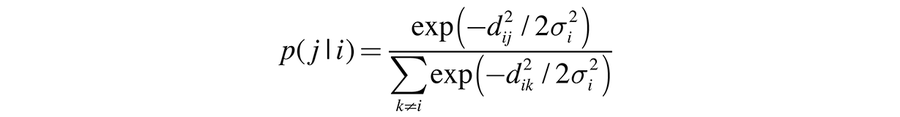
是選擇雪花 j 作為雪花 i 的鄰居的條件機率。
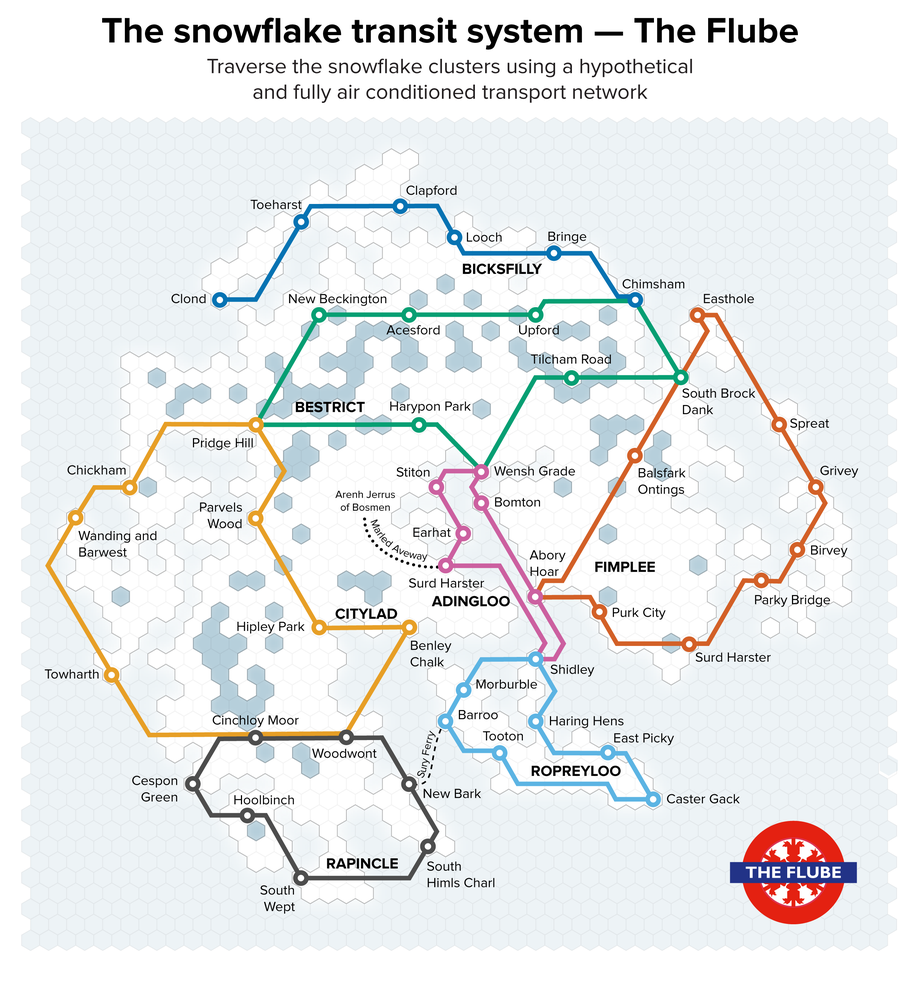
圖 6. 雪花二維 t-SNE 空間中的路徑集合,暱稱為“The Flube”。致謝:Martin Krzywinski 和 Jake Lever
我們已經使用 t-SNE 構建了一個雪花世界——一種通常有助於具體說明聚類之間關係的視覺化過程——我們想到擴充套件這片想象中的土地,使其擁有自己的交通系統,該系統將在這個大陸上形成一個網路,使雪花能夠在各個區域之間通行。自然而然地,我們將這個系統命名為“The Flube”(圖 6)。
由於雪花是模擬的,我們還使用在 622 個倫敦地鐵和鐵路站名稱上訓練的迴圈神經網路 (RNN) 模擬了 The Flube 中線路和車站的名稱。我們根據名稱的感知個性將名稱分組到線路中:Ropreyloo 充滿趣味性,車站如 East Picky 和 Morburble;Citylad 很時髦,車站如 Benley Chalk 和 Wanding & Barwest;而 Bicksfilly 沿線的 Bringe 和 Clapford 等車站不太可能是受歡迎的旅遊目的地。
RNN 是馬爾可夫模型的更復雜版本,馬爾可夫模型是一種有限狀態自動機,可以根據從字母(或單詞)訓練集中學習到的特定機率生成字母(或單詞)。轉移的機率僅基於機器的當前狀態,而不使用所有先前的輸出。另一方面,RNN 將傳統神經網路與內部狀態相結合。此狀態跟蹤網路的所有先前輸入,因此會記住生成單詞中的先前字母。RNN 概念已用於生成類似莎士比亞的英語、食譜和說唱歌詞。
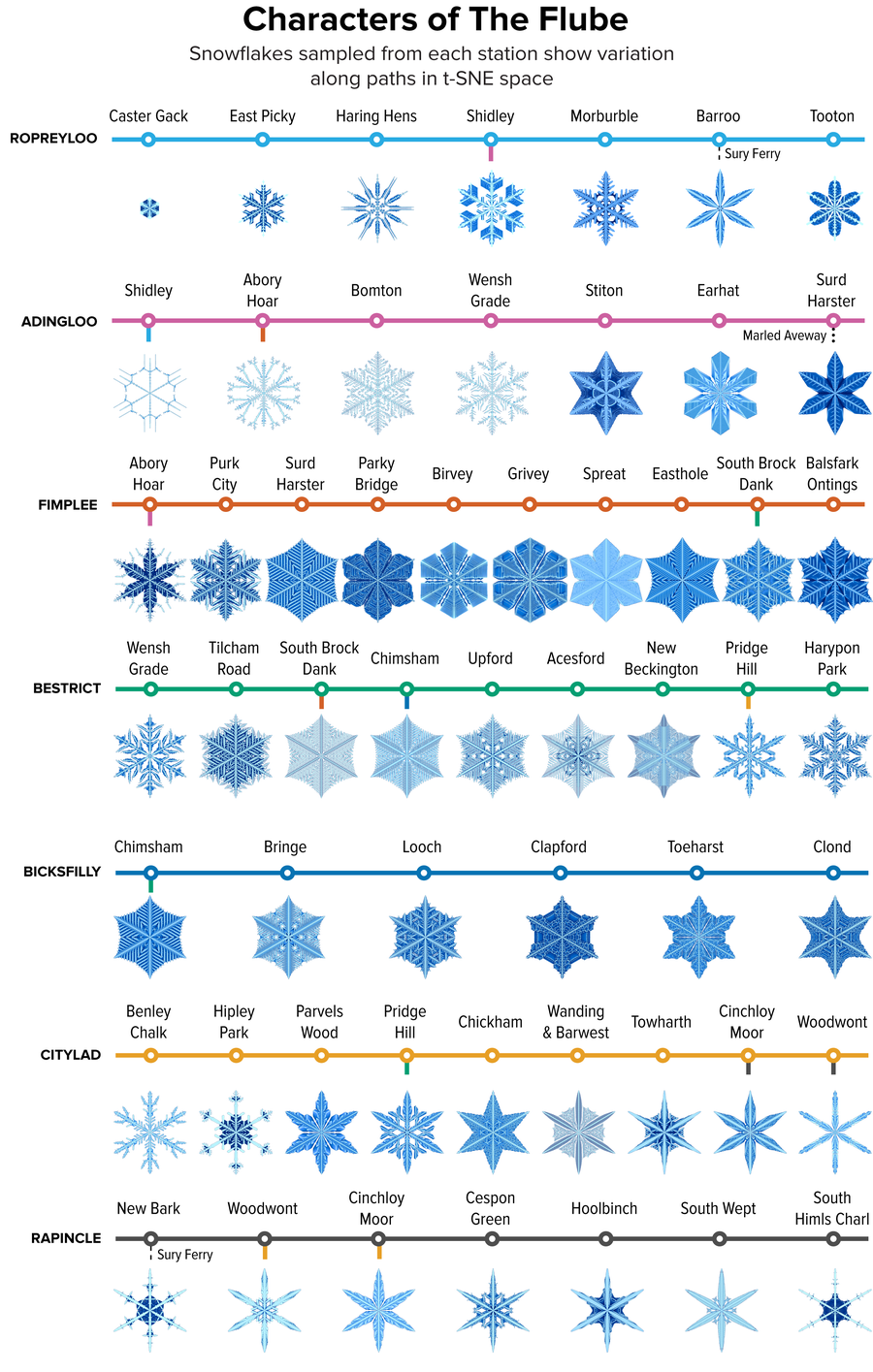
圖 7. The Flube 中每個車站的 t-SNE 六邊形網格中發現的雪花樣本,顯示了聚類內部和聚類之間的形狀變化。致謝:Martin Krzywinski 和 Jake Lever
我們可以使用 Flube 線路和車站來取樣 t-SNE 空間(圖 7),就像圖 2 中顯示的引數空間取樣一樣。我們根據我們對雪花形狀的印象分配了線路和車站名稱。較小(年輕)的雪花被分配了有趣的 Ropreyloo 線路,而北部的雪花,我們認為那裡是偏遠而嚴酷的土地,則獲得了 Bicksfilly。從 Caster Gack 到 Clond 的路程很長(需要四次換乘:Shindley、Abory Hoar、South Brock Dank 和 Chimsham)。
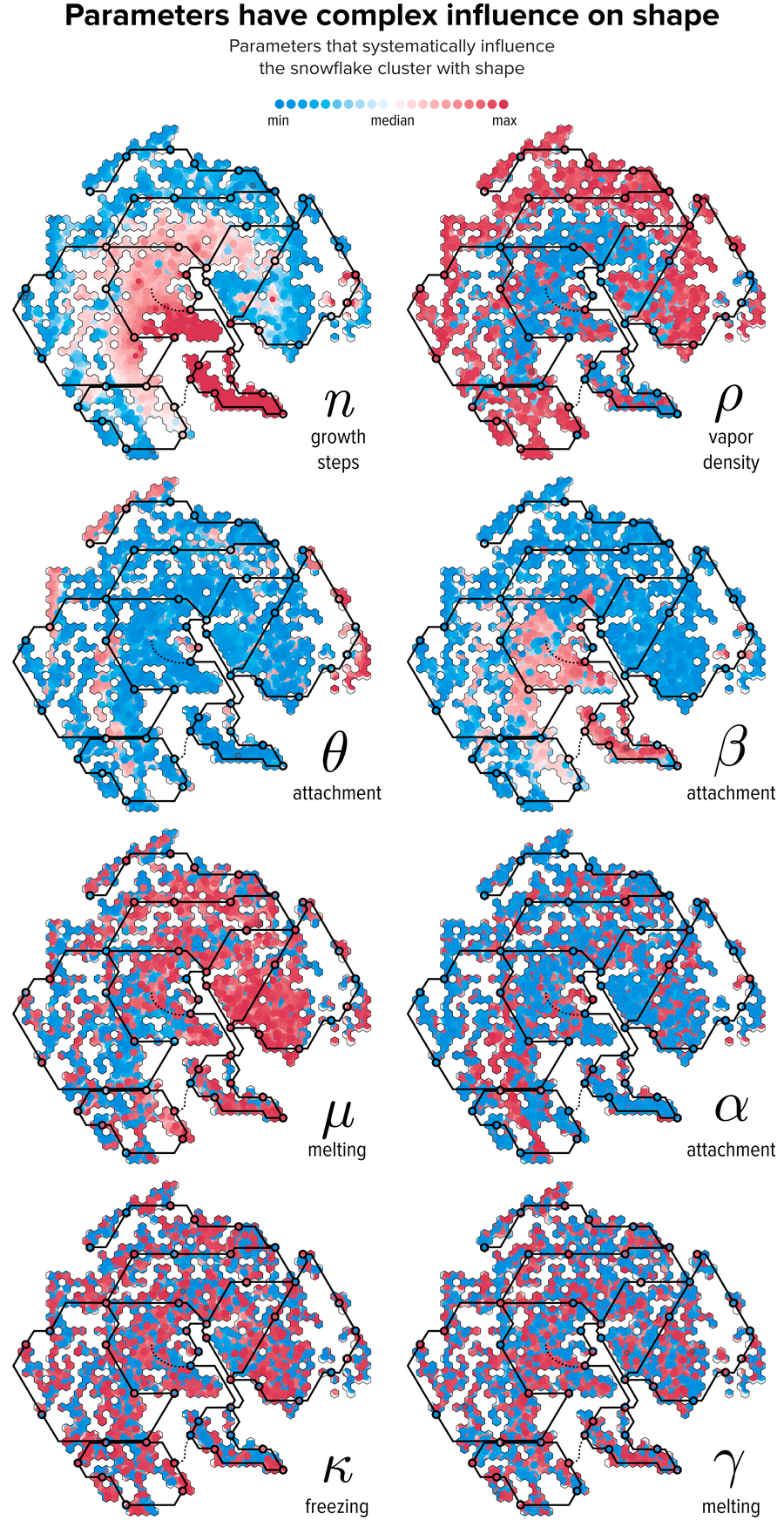
圖 8. 引數值與 t-SNE 聚類之間的關係。每片雪花都繪製成一個圓圈,顏色由雪花引數與中位值的相對差異決定。疊加了 The Flube 的線路,以幫助解釋圖 7 中的形狀變化。致謝:Martin Krzywinski 和 Jake Lever
圖 8 將引數值與 t-SNE 聚類聯絡起來。t-SNE 大陸上的雪花形狀現在可以透過其引數來解釋。例如,南部(Ropreyloo)帶有小雪花的島嶼對應於低 θ 和低 ρ,高 α 和高 β。北部半島(Bicksfilly)和東部島嶼群(Fimplee)帶有星狀板雪花(高 θ)。陸地中心(Bestrict)主要由蕨狀枝晶(低 ρ)組成,而西南次大陸(Rapincle)有許多星狀枝晶(低 α)。
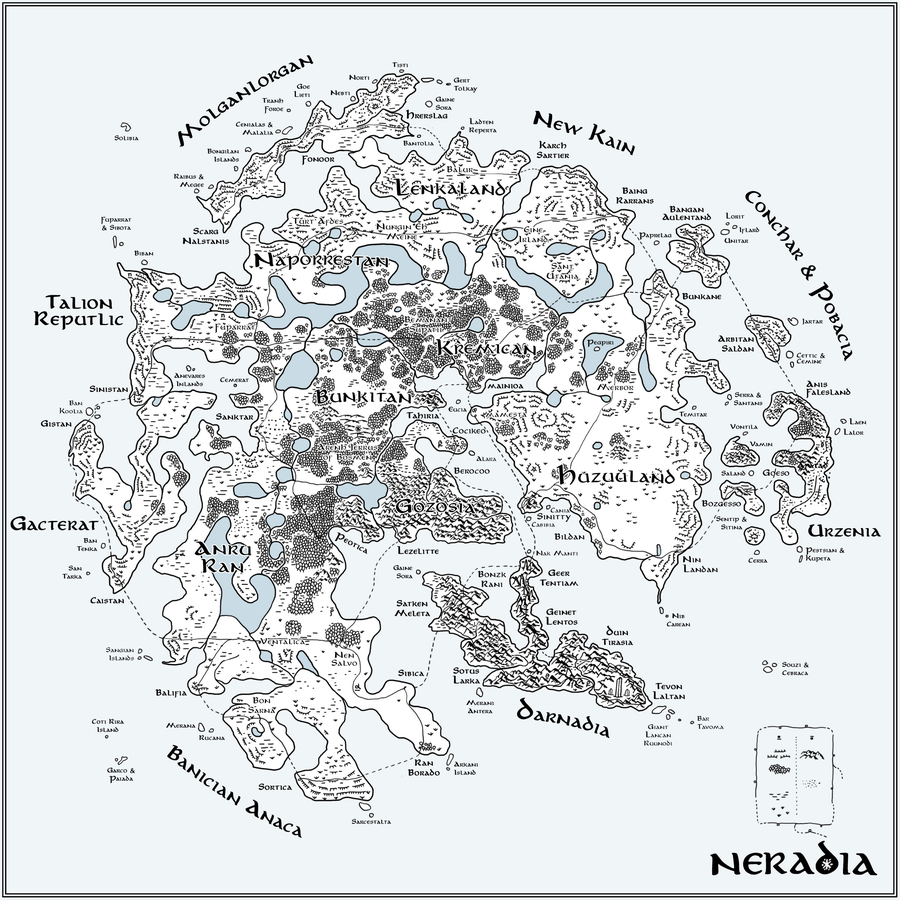
圖 9. 圖 5 中 t-SNE 地圖的手繪解釋。地理特徵編碼引數值:森林(低 ρ)、草原(低 β)、沼澤(低 μ)和沙漠(高 θ)。雪花生長的速度(達到完全大小的步數,n)由山脈(高 n)和冰崖(低 n)編碼。所有名稱均使用在 257 個國家/地區名稱上訓練的 RNN 生成。Flube 網路繪製為細線,車站為環路,城市(中等大小文字)放置在圖 6 中車站位置的位置。致謝:Martin Krzywinski 和 Jake Lever
一旦我們建立了交通系統,下一步就是想象一個完整的世界,我們稱之為 Neradia。透過將引數值編碼為地理特徵並使用在 257 個國家/地區名稱上訓練的 RNN,我們生成了圖 9 中 t-SNE 地圖的手繪版本,風格類似於托爾金。
即使使用像 257 個國家/地區名稱這樣的小型訓練集,RNN 輸出也非常有趣。我們最喜歡的是 Conchar & Pobacia(東北)和 New Kain(北部)地區。The Flube 中每個車站的位置都分配了一個城市名稱,以保持車站名稱的風格。Clapford 車站位於 Molganlorgan 地區的 Hrerslag 市,Abory Hoar 位於 Huzuuland 地區的 Sinnity 市。RNN 對字母的奇怪失誤,例如將“islands”變為“inlands”,出現在“Anevares Inlands”中,後者是 Talion Reputlic 地區深處的一組島嶼(一個滑稽的拼寫錯誤)。
我們已經在一個名為“unwords”的集合中探索了使用 RNN 生成其他文字。你的朋友勸阻你不要將你的第一個女兒命名為 Ginavietta Xilly Anganelel,但你沒有聽。當你將你的第二個女兒命名為 Nabule Yama Janda 時,每個人都想知道你擁有如此成功的孩子的秘訣是什麼。男孩也有很多選擇:Babton Laarco Tabrit 和 Ferandulde Hommanloco Kictortick。讓我們希望沒有人患有 myconomascophobia,永遠不會被 cakmiran 咬傷,並渴望成為 gabdologists。
圖 1 中的示例雪花被分配了來自 Bosmen 的 Arenh Jerrus 的 RNN 輸出,並根據其在 Bunkitan 地區森林中的 t-SNE 位置繪製在地圖上。這片雪花在 The Flube 地圖上足夠重要,擁有其專用連線線,稱為 Marled Aweway,它起源於 Adingloo 線路上的 Surd Harster。
下次當您身處暴風雪中或辛勤地剷雪時,請向 Neradia 的居民問好,並思考一個關於您自己資料的故事。
我們要感謝 Lisa Shiozaki 和 Rodrigo Goya 的有益討論。本文中包含的影像的高解析度版本可以在 Krzywinski 的網站上檢視。
