本文發表在《大眾科學》的前部落格網路中,反映了作者的觀點,不一定代表《大眾科學》的觀點
最近在資訊圖表和故事敘述方面的一些嘗試激發了我將幾何形狀視為人類在社會中的象徵。在科學和資料視覺化領域,線條、圓形和矩形等圖形無處不在。的確,從散點圖上的點到圖表上的條形,基本形狀通常充當視覺交流的語言。有時它們甚至被用來代表人。但是,當形狀變得生動起來,當它們實際上變成人的時候會發生什麼呢?事實證明,不起眼的多邊形可能會教會我們很多關於我們自己和我們所居住的世界的知識。
多邊形的寓言
上週,我參加了OpenVisConf,這是一個以在網路上視覺化資料為中心的年度波士頓活動。在眾多傑出的演講者中,有尼基·凱斯,他發表了一個題為“如何在 134 個簡單步驟中模擬宇宙”的精彩演講。尼基的演講主要關注將系統視覺化作為理解我們的世界和促進社會變革的起點。“多邊形的寓言”是一個關於種族隔離的互動探索,它很好地展示瞭如何以友好的“可玩”格式視覺化資料可以超越講述故事,並實際激勵使用者嘗試影響改變。

圖片來自尼基·凱斯和維·哈特的“多邊形的寓言”
單擊影像啟動互動
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保關於當今塑造我們世界的發現和想法的具有影響力的故事的未來。
我建議您一直滾動瀏覽並與視覺化內容進行互動,但為了本文的目的,我將總結基本前提。遊戲中的角色,即三角形和正方形,每個都表現出快樂、悲傷或“還行”的樣子。使用者的角色是將悲傷的角色移動到可用的空間,直到面板上不再有皺眉的臉。關鍵在於,所有形狀都希望處於相對多樣化的環境中。每個人的理想情況是,在其周圍區域中有三分之一的形狀看起來像他們。他們會接受來自自己群體的更高比例的鄰居,但如果被超過三分之二的鄰居包圍,他們會皺眉和搖晃,直到他們被重新安置。當所有形狀都對它們的鄰居感到滿意時,遊戲結束。

遊戲完成後,“多邊形的寓言”的影像
人們可能會認為,由於每個人都喜歡一定程度的多樣性,各組最終會相當好地融合在一起。然而,由於它們最初是有些隔離的,並且它們中的許多人被動地接受這種情況(就像在許多現實世界的社群中一樣),結果令人相當失望;幾乎不可能避免同質的區域。儘管每個人都只是“稍微有點形狀歧視”,但該系統實際上註定他們會得到一個不太理想的結果。遊戲的後續迭代表明,簡單地降低對另一組成員的偏見並不會有任何改變。相反,個人必須拒絕預設的隔離場景,並積極開始尋找看起來與自己不同的鄰居。
平面國
使用二維幾何形狀來代表寓言中的人物的想法並不新鮮。1884 年,一位名叫埃德溫·A·艾博特的英國教師出版了插圖小說《平面國:多維羅曼史》。艾博特的故事最初是作為關於維多利亞時代英格蘭的社會諷刺而提出的,但後來因其對假設的四維現實的思維實驗式調查而受到科學家和數學家的讚揚。

《平面國》的封面
由埃德溫·A·艾博特撰寫並繪製插圖
我再次敦促您自己閱讀這個故事——它既冷靜幽默又與當前的社會和經濟狀況驚人地相關——但如果您不能馬上放下一切去閱讀一本簡短的小說,請允許我概述一些關鍵點。主角是“一個正方形”,他住在平面國,之所以這樣命名是因為它是一個二維世界。平面國的社會是根據形狀劃分為嚴格的等級。男性是具有可變數量邊的多邊形;一個人的邊越多,他的等級就越高。因此,最高的社會等級由圓形組成。然而,女性都是簡單的直線——最低的階層。(頗具預見性的是,女性被認為是“缺乏理性但情感豐富”,被剝奪了受教育的權利,並被降級為家庭,以免粗心的多邊形在街上撞到她,並意外地被她尖銳的末端刺傷。)
表面上,晉升到這個等級是觸手可及的——至少對男性來說是這樣。根據所謂的“自然法則”,每一代等邊的多邊形都會增加一條邊。然而,這種進步的可能性逃脫了最低階層——等腰三角形的大多數成員。由於它們的邊和角不相等,它們必須首先上升到等邊狀態——只有最傑出的人才能應對這一艱鉅的挑戰——然後它們的兒子才能獲得更多的邊並改善他們在世界上的地位。
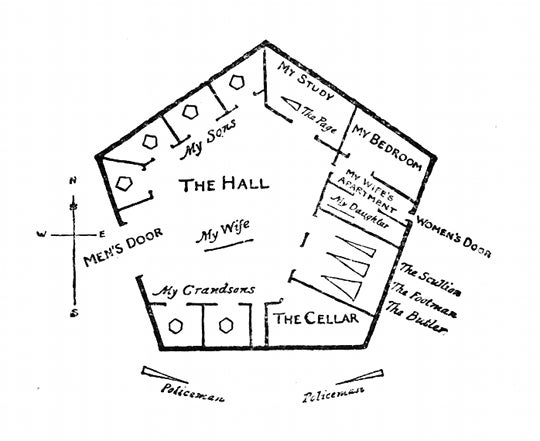
平面國中一個正方形的房子的插圖
當一個正方形做夢去了一個叫做線國的一維世界時,故事變得有趣起來。他試圖向線國的一位居民(一條線)解釋第二維的概念,結果遭到了完全的懷疑。(順便說一下,他線性的熟人原來是一位國王,他很生氣,因為這個正方形最初把他誤認為女人,在他的世界裡,女人不過是一個點而已。)正方形從他的幻覺中回來,為這條線無法理解這樣一個看似簡單的概念而感到惱火。

一個正方形與線國國王相遇的插圖
後來,在新千年的前夜,一個來自三維空間國的球體拜訪了一個正方形。當然,這個正方形最初是困惑的,無法想象第三維。這個正方形的無知使這個球體感到沮喪,他把這個正方形帶到了空間國,在那裡他能夠看到和體驗球體一直試圖用言語描述的東西。最後,一切都變得清晰起來。受到他對三維空間的新理解的啟發,這個正方形開始想象有四維、五維甚至更多的世界。但是,當他回到平面國並試圖將這些想法傳達給他的多邊形同胞時,他遇到了困惑和不信任。更重要的是,圓形委員會主席認為他的激進想法是對社會秩序的威脅,並將他投入了監獄。

平面國中的球體插圖
有趣的是,儘管艾博特對英國社會的精明批判在他那個時代基本上沒有受到賞識,但這本書中更多與科學相關的主題在 1915 年阿爾伯特·愛因斯坦發表他的廣義相對論後再次出現。從那時起,多年來,包括《大眾科學》在內的各種論壇中,令人欽佩的物理學家和數學家都引用了《平面國》。例如,在 1962 年,馬丁·加德納將他的“數學遊戲”專欄奉獻給分析“關於二維生活中虛構的故事”。就在 2012 年,史蒂芬·卡里普在描述引力在二維世界中的表現時引用了《平面國》。

2012 年 3 月刊《大眾科學》中“平面國中的量子引力”的圖形
馬爾科姆·戈德溫插圖
共同主題
儘管“多邊形的寓言”和《平面國》與非常不同的時代、地點甚至媒體型別相關聯,但它們之間的相似之處並不難發現。例如,在所描述的兩個社會系統中,積極變革的明顯潛力都依賴於錯誤的邏輯。“寓言”中的形狀假設它們對多樣性的個人偏好足以推動它們的社會走向融合,但事實證明它們所處的社會系統禁止這樣做。同樣,在《平面國》中,“自然法則”聲稱允許社會流動,但由於對下層階級的限制,很大一部分人口仍然永久處於邊緣地位,社會正義無法盛行。
此外,在這兩個世界中,真正的進步都需要比預期更積極、更戲劇性的轉變。在《平面國》中,一個正方形必須改變他對空間的整個概念,才能超越他狹隘的二維存在;事實上,他必須實際離開平面國並體驗另一個世界。同樣,在“寓言”中,自滿的正方形和三角形必須放棄他們對“形狀歧視”本質的先入之見,並對融合採取新的積極姿態。
故事的寓意:視覺化是關鍵!
令我高興的是,這兩個故事都提倡將視覺化作為理解社會本質的關鍵。“多邊形的寓言”以更直接的方式呈現了這個概念,因為形狀的物理排列會根據使用者的操作而明顯變化。在《平面國》中,視覺化案例更具概念性;這個正方形直到看到和體驗過三維世界之前都無法想象。但除此之外,在講述他的故事時,多邊形敘述者為讀者提供了圖表。
更具說服力的是,在文章的結尾,A Square 哀嘆他無法向同伴解釋三維空間,因為他缺乏一個可用的繪圖表面。艾勃特寫道:“所以我花了幾個月的時間私下撰寫了一篇關於三維奧秘的論文……我說的不是一個物理維度,而是一個思想領域,理論上,一個圖形可以從那裡俯視平面國,並同時看到所有事物的內部,並且在那裡可能被認為存在一個被六個正方形包圍,幷包含八個端點的圖形。但在撰寫這本書時,我發現自己因無法繪製我目的所需的圖表而感到非常沮喪;因為當然,在我們平面國的國家裡,沒有平板,只有線條,也沒有圖表,只有線條,所有都在一條直線上,只能透過大小和亮度的差異來區分;所以,當我完成我的論文時……我不能確定很多人會理解我的意思。”
所以,你看到了。理解並最終改變世界的關鍵在於我們視覺化支配我們的系統的能力。幸運的是,我們的四維世界賦予了我們這種能力,當我們尋找符號來表示系統的組成部分時,可靠的小形狀將在那裡幫助我們。