本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
對於猶他州人來說,欣賞戶外風光幾乎是合同規定的。我的德克薩斯州血統至今阻止我成為一名滑雪者——徒步旅行更符合我的節奏。徒步旅行給了我很多:鍛鍊、新鮮空氣、野生動物和有趣的岩石景觀,偶爾還能讓我對某個數學問題產生新的看法。最近一次徒步旅行中,我和我的配偶高估了我們的耐力,低估了我們選擇的 trail 的難度,我對芝諾悖論有了更深刻、更發自內心的理解。
大約2500年前,埃利亞的芝諾提出了一些相關的悖論,討論運動是否是一種幻覺。我在徒步旅行中思考的那個悖論有時被稱為二分法悖論,當人們在談話中提到芝諾悖論時,這可能是大多數人想到的那個。它是這樣的:為了從 A 點到達 B 點,你必須首先跨越 A 點到 B 點距離的一半,然後跨越剩餘距離的一半,然後再跨越從該點開始的剩餘距離的一半,依此類推。你永遠無法到達目的地,因為你必須在旅途中訪問無數箇中間點。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞事業 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和思想的具有影響力的故事。
深入探討這個論點,即使是為了到達中點,我們仍然有另一個芝諾悖論需要克服。我們必須到達中點的一半,以及該點的一半。這種推理似乎暗示運動是不可能的。然而,我們的生活和我們的徒步旅行證明了我們確實可以從 A 點到達 B 點。
對於剛入門的數學家來說,這個悖論通常是他們最初接觸無窮概念並與我們有限的人類在試圖理解它時遇到的內在矛盾作鬥爭的地方。但是,儘管芝諾悖論很流行,但它對我來說從來沒有真正產生過沖擊。當我第一次遇到它時,我太務實了——顯然我可以走過房間,所以我們為什麼要擔心這個呢?它對我來說總是顯得有點傻。直到那次徒步旅行。
那次徒步旅行是我們兩天內的第二次艱難徒步。我的小腿肌肉又緊又痠痛。我的腳上好幾處都起了水泡,每走一步都變得更加疼痛。我的揹包帶和汗溼的襯衫摩擦著我的肩膀和臀部。在我們所在的高度,海拔超過 10,000 英尺,每一次呼吸都感覺不足,每一步都是來之不易的勝利。最重要的是,我有點想小便了。
我開始痴迷地檢視徒步旅行應用程式上的 GPS。每次檢視時,我都會進行一些心算。到山頂還有多遠?當我們掉頭後,我還剩下多遠的路程?在我回到 trail head,享受堆肥廁所和汽車舒適座椅帶來的幸福解脫之前,我必須先走到一半的路程。那是在過溪流之前還是之後?一旦我們到達中點,我們就必須走完返回 trail head 的剩餘距離的一半,併到達危險的陡峭之字形路段。一旦我們到達那裡,我們仍然需要到達 trail head 距離的一半。就在那時,我們看到了兩隻駝鹿——一隻母鹿和它看起來笨拙,但仍然巨大而有力的幼崽——當我們默默地站在 trail 旁邊,等待動物們吃飽並離開時,悖論似乎更加真實了。
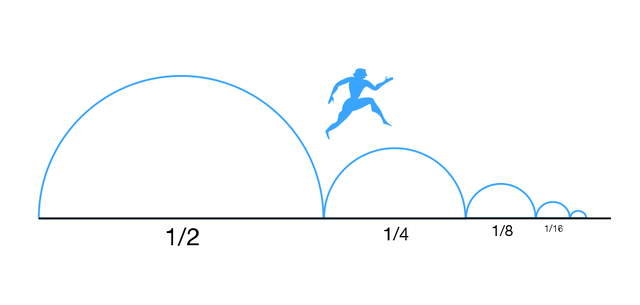
從數學角度解釋和解決芝諾悖論並不太難。亞里士多德指出,隨著距離的減小,所需的時間也會減少。今天,我們可以使他的論點更加精確,寫下無窮級數的和,有時甚至從中得到一個有限的數字。在芝諾悖論的情況下,我們可以將這種情況表示為 1/2+1/4+1/8+1/16+… 的和,它加起來等於數字 1。因此,如果我們以恆定的速度移動,或者即使我們感到疲倦但仍以快於某個最小速度的速度繼續前進,我們最終將跨越兩個地點之間的距離。
在 trail 上,解決芝諾悖論不是一個總結漂亮的幾何級數的問題。而是在於不顧水泡、摩擦、稀薄的空氣以及在舒適的岩石上休息片刻的誘惑,大膽地一隻腳接一隻腳地向前邁進。
有關芝諾悖論的更多資訊,請檢視 BBC 廣播節目《In Our Time》的最新一集,或檢視 Vi Hart 關於微積分和人行橫道的有趣影片。有關另一位“山上的芝諾”,請檢視我的數學上的哥哥 Zeno Huang,他也喜歡在美國西部各州徒步旅行。
