本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
今年早些時候,瑪麗娜·維亞佐夫斯卡展示瞭如何在八維空間中最有效地排列球體。嘗試思考高維空間可能令人困惑,但數學家們為此掌握了一些技巧。正如三維空間可以使用三個座標——長度、寬度和高度,或 (x,y,z)——來標記一樣,八維空間使用八個座標。我們可以透過新增更多座標來研究的維度數量沒有限制。在任何維度中,球體都是一組到某個中心點距離都相同的點。在二維空間中,球體是一個圓,在三維空間中,它是我們通常認為的球體。
由於高維空間對於我們來說即使不是不可能視覺化,也很困難,因此很容易認為它們沒有任何現實世界的意義。然而,令人驚訝的是,它們可以非常自然地出現。
它們自然出現的一種方式是在縫紉中,這是我本月早些時候寫過的。在我的關於維亞佐夫斯卡球體堆積突破的文章中,我提到了高維球體堆積的另一個應用:資料傳輸和糾錯碼。
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們今天世界的發現和想法的具有影響力的故事的未來。
情況如下:我們想透過一個通道傳輸訊息,資料在傳輸過程中可能會損壞。在現實世界中,想想手機或光纖電纜,甚至只是試圖在嘈雜的房間裡進行對話。我們的想法是找到一種通訊方式,使其能夠抵抗傳輸資料中的微小變化。
以 北約音標字母為例,它更廣為人知的名稱是它的前三個詞,alpha-bravo-charlie。如果您必須透過電話拼寫您的名字,那麼另一端的人很容易將 B 誤認為 P,因此能夠說“B 代表 bravo”很有幫助。音標字母中代表字母的單詞經過選擇,即使有很多靜電,也不會對您指的是哪個字母產生任何歧義。您永遠不會說“B 代表 bad”,這可能會讓對方感到困惑:“D 代表 dad?P 代表 pad?”
糾錯碼就像音標字母一樣,是一種編碼資料的方式,即使資料在傳輸過程中被更改,也允許人們重建訊息。 一種方法是僅選擇有限數量的可能訊息進行傳輸,並構建一些冗餘。 例如,如果我們只想傳輸訊息“yes”和“no”,我們可以決定將“yes”編碼為 111,將“no”編碼為 000。 如果我們收到訊息“101”,我們可以假設其中一個數字在傳輸過程中已損壞,但仍然可以推斷出傳送者打算說“yes”。 當然,此程式碼並非完美。 如果兩個數字被損壞,我們將最終誤解答案,但這肯定比沒有好。
當我們嘗試為傳送更復雜的訊息尋找糾錯碼時,球體堆積就派上用場了。 在這種情況下,我們可以將我們正在傳輸的資料視為高維空間中的一個點。 例如,如果我們想傳輸每條訊息包含 100 條資料的訊息,我們可以將我們的訊息視為 100 維空間中的點。 每個座標都是其中一條資料。
我們的目標是在 100 維空間中找到一組好的點,我們可以將其用作碼字。 我們希望我們的碼字做什麼? 好吧,如果某些資料片段略有更改,我們希望碼字仍然可以識別,因此我們不希望我們的碼字太相似。 在 100 維空間中,這相當於每個碼字都是一個具有某個小半徑的 100 維球體的中心。 傳送訊息的人將傳輸其中一個球體中心的座標作為他們的碼字。
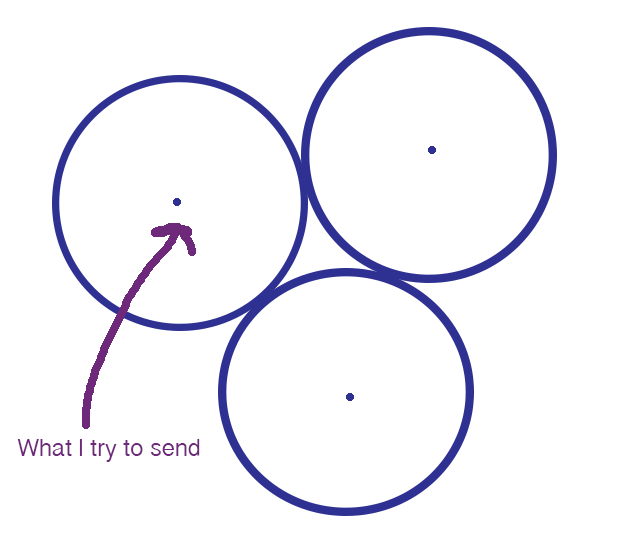
我還沒有獲得可以繪製 100 維球體的 Adobe 升級版,因此這張二維示意圖將不得不湊合使用。 圖片來源:伊芙琳·蘭姆
如果點的座標在傳輸過程中略有更改,則接收者將收到與傳送者傳送的訊息略有不同的訊息。
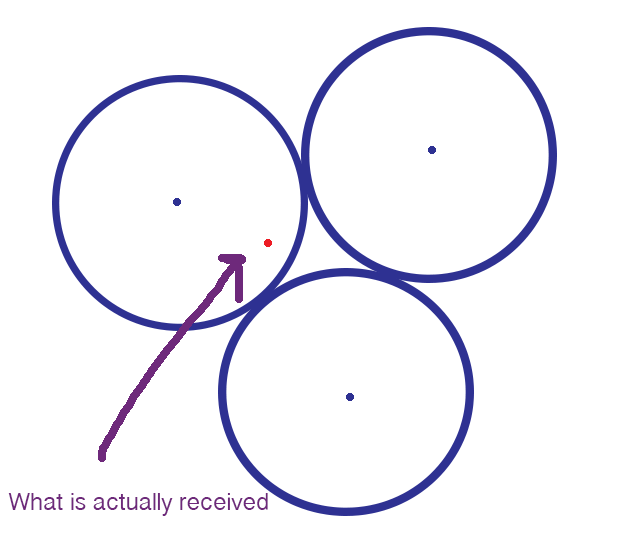
圖片來源:伊芙琳·蘭姆
但是,如果訊息仍然非常接近預期訊息,則接收者將知道預期訊息是什麼並正確解釋訊息。 幸運的是,在上面的圖表中,錯誤訊息與我打算傳送的訊息之間的距離很小,因此接收者將正確解釋它。
球體堆積問題詢問我們如何在例如 100 維空間中儘可能密集地堆積等尺寸的球體。 對於糾錯碼,這些球體的中心是我們的碼字。 半徑的選擇將基於我們認為我們的傳輸方法可能會在傳送訊息時晃動訊息的程度。 如果我們認為錯誤的累積效應——每個點在傳輸中可能被推離多遠——最多為 1 個單位,我們將考慮堆積半徑為 1 的球體。 如果可能是 3 個單位,我們將堆積半徑為 3 的球體。 但是,半徑是多少並不重要。 這是一個數字,我們將根據我們的傳輸技術的工作方式來選擇它。
因此,我們正在尋找 100 維空間中的球體,它們的半徑彼此之間都相距一定距離。 驚喜! 我們剛剛在其自然棲息地中找到了一個球體堆積問題。 解決 100 維空間中的球體堆積問題相當於弄清楚我們可以在 100 維空間中的某個定義區域中堆積多少碼字。 我們堆積碼字的效率越高,我們可以使用我們的 100 維訊息方案發送的獨特訊息就越多。 這就是為什麼解決球體堆積問題可能對資料傳輸產生重要的實際影響。
人們可能會合理地問,解決球體堆積問題對於尋找糾錯碼有多重要。 我們看到球體堆積問題是解決糾錯碼的一種方法,但也許我們是否找到最有效的方法來堆積它們並不重要。 相當好就足夠了嗎?
高維球體變得尖銳。 這是一種異想天開的方式來描述關於高維球體的兩個相關事實:直徑為 1 的球體在我們維度升高時,在邊長為 1 的立方體的體積中所佔的比例越來越小,並且最佳球體堆積的密度隨著維度的增加而降低。 在二維空間中,我們可以用蜂巢式最佳六邊形堆積用圓填充大約 91% 的平面。 有效堆疊的橘子可以填充大約 74% 的三維空間。 球體堆積問題在四維空間中尚未解決,但在八維空間中,維亞佐夫斯卡表明,最密集的堆積填充了大約 25% 的空間,而在 24 維空間中,最佳堆積僅填充了 0.1% 的空間。 事實上,雖然我們不知道除二、三、八和 24 維之外的任何維度的確切答案,但我們確實知道球體堆積密度的上限隨著維度的增加呈指數級下降。
高維球體的尖銳性意味著,即使在 100 維空間中有很多空間,當我們嘗試製作糾錯碼時,我們也不能很好地將碼字塞進去。 因此,找到最佳球體堆積變得更加重要,這樣我們才能儘可能多地從(或進入?)難以填充的空間中獲得。
維亞佐夫斯卡在八維球體堆積方面的突破——以及隨後的 24 維問題解決方案——對使用這些維度建立糾錯碼沒有實際影響。 研究人員已經知道正確答案在百分之幾的誤差範圍內,因此任何在這些維度中堆積球體的人都已經使用了正確的模型。 但她的工作證明了一種新穎的球體堆積方法有可能在其他維度上發揮作用,並對我們彼此溝通的方式產生重大影響。