本文發表於《大眾科學》的前部落格網路,反映作者的觀點,不一定反映《大眾科學》的觀點。
我一直認為《蒙娜麗莎》作為連點成線謎題會更好,難道你不覺得嗎? 幸運的是,對我們來說,歐柏林學院的數學家羅伯特(鮑勃)·博世和計算機科學家湯姆·韋克斯勒正在開創一種新技術,可以將您最喜愛的傑作變成由點和交叉線組成的複雜圖案。他們稱之為具象巡迴問題(FTP)。他們關於該方法的初步論文將發表在2015 Bridges數學-藝術會議的論文集中,目前可在博世的網站上線上獲取。
這項新技術是對現有最佳化藝術流派的擴充套件。 最佳化藝術使用計算約束來生成有趣的影像。多米諾骨牌肖像和馬賽克是一種形式,但與FTP最接近的最佳化藝術類似物是旅行商問題(TSP)藝術。旅行商問題的目標是找到穿過任意一組點的最短路徑,就像旅行推銷員在可以輕鬆建立Etsy商店之前的黑暗日子裡可能走過的路徑一樣。
為了創作TSP藝術,您需要將所需的圖片變成一片聚集的點,然後讓計算機找到它們之間TSP最優路徑,如下圖所示。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道: 訂閱。透過購買訂閱,您將有助於確保未來能夠繼續報道有關發現和塑造我們當今世界的想法的具有影響力的故事。

左圖:蒙娜麗莎TSP的點簇。右圖:最優路徑。 來源:羅伯特·博世和湯姆·韋克斯勒
正如博世和韋克斯勒寫道:“即使這條路徑是可能的最佳路徑,並且確實與目標影像相似,但它並沒有像單獨的點那樣達到良好的相似度。” 僅僅為了讓圖片變得更糟而解決旅行商問題似乎有點浪費,因此他們決定改變遊戲規則。
他們沒有在影像中聚集點,而是從規則的點網格開始。然後,遊戲的目的是將它們連線起來,不是用解決旅行商問題的路徑,而是用在視覺上類似於目標影像的路徑。路徑仍然應該精確地擊中每個點一次,但現在獲勝的行程可能會比TSP最優路徑更長。
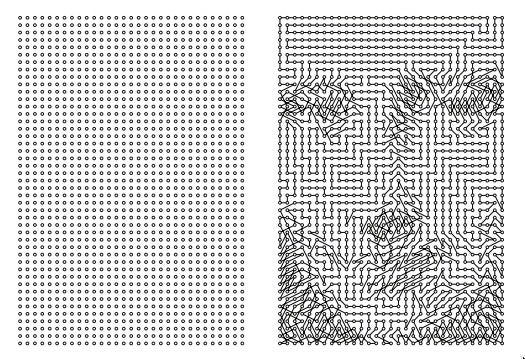
左圖:1395個點的網格。右圖:類似於蒙娜麗莎的具象巡迴。 來源:羅伯特·博世和湯姆·韋克斯勒
為了量化這個問題,博世和韋克斯勒將目標影像轉換為灰度影像,併為網格的每個點分配一個介於0和1之間的數字,該數字表示圖片在相應區域的深淺程度。經過一些實驗,他們決定將邊緣限制為國王或騎士的移動,並且進一步的實驗幫助他們確定如何為網格的每個部分分配權重,以對應邊緣使其變暗的程度。研究人員使用Gurobi最佳化器來尋找路徑,以最大限度地減少灰度目標影像和FTP影像之間亮度的總差異。

波提切利的《維納斯》作為具象巡迴。 來源:羅伯特·博世和湯姆·韋克斯勒
正如您可能想象的那樣,具象巡迴問題在計算上非常昂貴。 事實上,對於他們使用的網格尺寸,Gurobi 根本無法獲得良好的結果。(“我不是在責怪Gurobi,”博世在一封電子郵件中寫道。這是一個難題!)博世和韋克斯勒沒有嘗試在整個網格上最佳化路徑,而是決定分別檢視較小的塊,然後仔細地將他們為每個部分獲得的路徑拼接在一起,以找到整個網格的良好解決方案。 這個過程仍然需要很長時間,但至少它可以發生。“使用滑動視窗方法,我可以在一兩天內獲得一個像樣的具象解決方案,”博世寫道。
博世和韋克斯勒的論文還描述了一種類似的新最佳化藝術方法,稱為具象編織問題:他們不是用一條路徑連線網格中的所有點,而是在頂行的每個點開始一條路徑,並最終將每個頂部點連線到底部的一個點,在向下移動的過程中精確地擊中每行中的一個點。 這些線束彼此分離,因此,像辮子的線束一樣,它們從上到下交織在一起。 在我看來,這些影像看起來並不像FTP解決方案那樣像目標圖片,但彎曲的線條很獨特且在視覺上令人愉悅。 它們非常適合放在宿舍的牆壁上。

瑪麗蓮·夢露作為具有三種不同約束條件的具象編織問題的解決方案。 來源:羅伯特·博世和湯姆·韋克斯勒
對於理論計算機科學愛好者:博世尚未研究FTP的計算複雜性,但他的猜測是它是NP-hard難題。 這也是我的猜測;它似乎與TSP沒有太大區別——只是最佳化的函式略有不同,但問題的關鍵是相似的。 這只是一個猜測,但我喜歡繪製蒙娜麗莎是NP-hard難題的想法。
