本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點

一個牙膏管具有二維洞的演示。圖片來源:Slipp D. Thomson,透過 Flickr。
萬聖節時,我寫了一個非常可怕的話題:高階同倫群。同倫是拓撲學中的一個概念,拓撲學是數學的一個分支,研究形狀的屬性,這些屬性無論你如何擠壓或拉伸它們都保持不變,只要你不撕裂它們或將東西粘在一起。同倫群和稍微相關的同調群都是用代數描述形狀拓撲的不同方法。在我的文章中,我說同調檢測不同維度的“洞”。但是,正如一位評論員所問,我說的不同維度的洞是什麼意思?
好問題!我故意使用“洞”作為一個含糊的詞,因為“洞”沒有真正的數學定義。但這是我的簡短回答,這也是我不是代數拓撲學家的原因。如果你可以把它放在項鍊上,它就有一個一維的洞。如果你可以用牙膏填充它,它就有一個二維的洞。對於更高維度的洞,你就只能靠自己了。
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保未來能夠持續講述關於發現和塑造我們當今世界的想法的具有影響力的故事。
這個答案不是很令人滿意。有沒有更好的方法來描述洞?我和我的一些拓撲學家朋友交談,發現了兩件事:拓撲學家們對洞的定義並不完全一致,思考一個數學定義尚未完全確定的詞的不同解釋是既有趣又令人感興趣的。我認為我更大的結論,本著這個季節的精神,是洞就像聖誕老人:真正的意義在於你的心中。所以讓我們審視我們的內心,思考洞是什麼。
《斯坦福哲學百科全書》中有一篇關於羅伯特·卡薩蒂和阿基萊·瓦爾齊撰寫的有趣的關於洞的條目。它開頭是
對於本體論學家和認識論學家來說,洞是一個有趣的案例研究。對世界的天真、未經教導的描述將洞視為指稱的物件,與普通的物質物件相提並論。(“乳酪上的洞和錫罐裡的餅乾一樣多。”)我們經常求助於洞來解釋因果互動,或解釋某些事件的發生。(“水流出來是因為桶上有個洞。”)因此,有初步的證據表明這些實體的存在。然而,可能會有人認為,提到洞只是一種說法,洞只是純粹的表象實體,類似實體,虛構。
幸運的是,我們是數學家,而不是哲學家,所以我們不需要過多地擔心洞是否存在這種瑣碎的細節。(有些人也對聖誕老人採取這種態度。)
我必須警告你,這篇文章最終會有點迴圈論證。在某種意義上,n維洞的數學定義“應該”是導致n維同調群或同倫群中存在有趣的東西,或使其非平凡的東西。

一個籃球上有一個洞。圖片來源:公共領域,透過維基共享資源。
Mathworld關於洞的條目中,埃裡克·韋斯坦給出了一個我非常喜歡的定義:“數學物件中的洞是一種拓撲結構,它阻止該物件被連續地縮小到一個點。”
讓我們想想一個籃球。使用韋斯坦的定義,它肯定有一個洞,因為你不能在不改變其籃球性的情況下將其完全擠壓成一個點。
我喜歡這個定義,因為它很直觀,但我認為它有點危險,因為拓撲學中使用了幾種不同的連續縮小到點的概念,並且很容易將它們混淆。(相信我。我經歷過。)平面中的一個圓可以連續地縮小到一個點*,但直觀上,並且在同倫和同調的意義上,一個圓有一個洞。然而,這種縮小的概念依賴於圓位於二維平面中的假設,所以它實際上告訴我們一些關於平面的拓撲結構,而不是圓的拓撲結構。我們需要我們的定義不依賴於事物在空間中的位置。
韋斯坦的定義使用的縮小到點的概念要求我們始終保持拓撲等價。我們不能將一個圓縮小到一個點,因為我們最終會在最後撕裂或擠壓某些東西。
那麼定義洞的維度呢?這更棘手。一個誘人的定義,也是我一位拓撲學家朋友更喜歡的定義,是流形中的n維洞是流形“像”n維球體的地方。(為了我們的目的,一維球體是一個圓,二維球體是籃球形狀,依此類推。這是因為近距離觀察,圓看起來像一條線,球體看起來像一個平面。)更嚴格地說,物件中的n維洞是阻止n維球體到該物件的某些對映在不離開該物件的情況下縮小到一個點的東西。洞的這個定義意味著我們將洞性等同於同倫。讓我們研究一些例子。
首先,一個平面。你不能把它放在項鍊上,也不能用牙膏填充它,所以它可能沒有洞。讓我們檢查一下。有很多不同的方法將一個圓對映到一個平面,但所有這些方法都可以在保持在平面上的同時縮小到點。換句話說,在平面上滑動橡皮筋並儘可能縮小它沒有任何阻礙。所以根據我們目前的工作定義,平面沒有一維洞。這很好,因為如果平面有一個洞,那麼我們對洞的定義就是錯誤的。
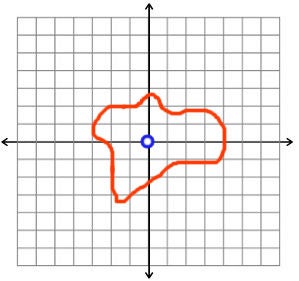
我們可以判斷穿孔平面有一個洞,因為我們無法將橙色環拉過缺失的點,藍色輪廓突出顯示了缺失的點。圖片來源:伊芙琳·蘭姆。
那麼移除一個點的平面呢?我們仍然不能用牙膏填充它,但是如果給定一條非常細的鏈條,我們可以把它放在項鍊上,所以它應該有一個一維洞。我們如何看到這一點?如果我們將一個圓對映到平面上,並且移除的點在圓內,我們就會遇到問題。(書呆子可能會指出,我沒有證明存在圓對映到平面內部和外部這樣的東西,無論有沒有洞。你是對的,你可以自己寫一篇關於它的部落格文章。我們其餘的人會假設我們可以找到一個足夠禮貌的圓對映,使其具有明確定義的內部和外部。)我們無法將圓拉過或縮小到該點,所以我們知道減去一個點的平面有一個一維洞。
現在回到我們之前談到的籃球。我們知道它有一個洞。它的洞是什麼維度?你不能把它放在項鍊上,但你可以用牙膏填充它,所以它可能是二維的。現在來檢查一下。它沒有一維洞,因為任何你把橡皮筋(或圓)放在籃球上的方式,你都可以把它縮小到一個點,而不會離開籃球的表面。但它確實有一個二維洞,因為你不能連續地將二維球體到該空間的每個對映都縮小到一個點,而不離開籃球。(為了選擇唾手可得的成果,如果你的從籃球到籃球的對映是恆等對映,即所有東西都停留在同一個位置,你就無法將其縮小到一個點。)
到目前為止,我們使用的洞的定義似乎很有希望。但最終,我認為它不是最好的定義。
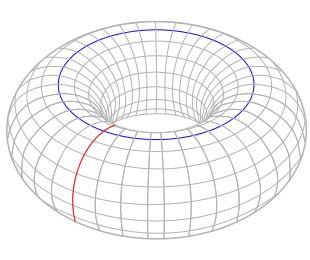
環面上的兩個突出顯示的環向我們展示了兩個不同的一維洞。圖片來源:YassineMrabet,透過維基共享資源。
讓我們看看環面,最簡單的拓撲空間之一。環面可以被認為是甜甜圈的釉或內胎的表面。我們可以把它放在項鍊上,也可以用牙膏填充它,所以它應該有一維和二維的洞。對於一維洞來說,一切都很好:基本上有兩種主要的圓的對映無法縮小到環面上的一個點的方式。要麼它可以繞著甜甜圈的洞(左圖中的藍色圓圈)轉,要麼它可以像你的手指如果穿過甜甜圈的洞並用你的食指抓住它所形成的圓圈(左圖中的紅色圓圈)。所以環面有兩個一維洞。(除非你站在環面內部佩戴其中一條項鍊,否則你不會用項鍊定義找到它們。)
當我們涉及到二維洞時,我們的工作定義就崩潰了。環面“應該”有一個二維洞,但我們無法使用二維球體的對映找到它。(這至少對我來說並不明顯。你可以考慮嘗試用氣球包裹內胎,以瞭解正在發生的事情。)
我們根據球體的對映對洞的定義不適用於環面中的二維洞,但我真的想說洞在那裡。我認為正確的答案,儘管它看起來不是特別有見地,是使用相同的定義來定義洞,但允許任何二維物體的對映,而不僅僅是球體。有一個二維物體我們可以對映到環面中,而不能在保持在環面上的同時縮小到一個點,它就是環面本身。所以如果我們知道環面在拓撲上不等同於一個點,我們就知道它有一個二維洞。這種定義看起來有點像“我看到它時我就知道它”的定義,並且在實踐中沒有太大幫助。如果我們對一個物體知之甚少,我們如何知道要將無限多的二維表面中的哪一個對映到其中以測試其聖潔性?但是這種概念的一個版本,更精確地定義,就是同調。(對於有雄心壯志的人,你可以在艾倫·哈切爾的免費代數拓撲教科書中閱讀更多關於它的內容。值得注意的是,哈切爾始終在“洞”這個詞周圍使用引號,因為他從未定義過它。)
定義同調有幾種方法,但對我來說最直觀的方法是採用一些基本構建塊——頂點、邊、面等等——並觀察它們如何粘合在一起形成表面。雖然它比這更微妙,但同調基本上告訴你某種維度的哪些構建塊沒有限定你空間中更高維度的構建塊。這與我們已經看到的洞的概念相符:環面中的兩個不同的洞來自(一維)圓,這些圓沒有圍繞空間中的(二維)實心圓盤轉動。二維洞來自於環面僅由二維和更小的元件組成的事實,因此其二維元件不限定表面的任何三維部分。另一方面,實心環面(整個甜甜圈)沒有任何二維部分不是三維部分的邊界,因此它沒有二維洞。(甜甜圈釉的二維洞現在被三維麵包填充。這比牙膏好多了。)

霍普夫纖維化的視覺化,這證明了一個令人驚訝的事實,即籃球有一個三維洞。圖片來源:Niles Johnson,透過維基共享資源。
數學家通常僅將同調稱為檢測洞,使同倫——以及我們早期對n維洞的工作定義——高高掛起。這個定義的一個優點是,我們永遠不會在低維空間中有一個高維洞,這是一個令人不安的前景,這也是我發現高階同倫群令人毛骨悚然的原因。如果我們允許基於同倫的洞的定義,那麼籃球就有一個三維洞。(所以我猜它可以被四維生物用來刷牙。)霍普夫纖維化,我在之前的文章中也提到過,是從三維球體到二維球體的對映,它不能縮小到一個點。
所以對於洞,你可以選擇你最喜歡的定義。我想我更喜歡使用同調定義,但是關於不同的洞檢測器可以檢測到不同的洞的想法有一些美妙之處,所以我可能會嘗試敞開心扉——為了簡單起見,我假設它在拓撲上等同於一個二維球體——並讓三維洞進入。
如果你堅持到這裡,你值得一份獎勵。一個裝滿西瓜果肉的二維球體沒有一維洞的演示怎麼樣?
感謝Arunima Ray和兩位克里斯托弗·戴維斯(Christopher Davis?)對這篇文章的有益評論。任何你不喜歡的地方都是我的錯。
*在平面中將圓縮小到一個點的秘訣:從半徑為 1 的圓開始,為了方便起見,將其設定在點 (0,0)。我們將定義一個雙變數縮小對映。第一個變數將表示圓上的一個點,我們將透過角度(從 x 軸逆時針測量)來識別它。第二個變量表示時間。我可以使用對映F(a,t)=(1-t)a在從 0 到 1 的時間間隔內將任何圓縮小到一個點。在嚴格介於 0 和 1 之間的任何時間w,此對映的影像都是半徑為1-w的圓。在時間 1,我們有一個半徑為 0 的“圓”,這也稱為一個點。像這樣的對映一直被用作路徑之間顯式同倫的示例。