本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
我對連分數了解得越多,就越為之著迷。 上週,當我寫到連分數比我們通常用來描述數字的任意十進位制數字好多少時,我提到連分數告訴我們無理數的“最佳逼近”。 連分數只是由分陣列成的分數。 每個數字,無論是有理數還是無理數,都可以寫成連分數。 為了獲得編寫它們的系統方法,現在我們將專注於分子中只有 1,分母中只有正整數的連分數,儘管有些非常漂亮的連分數不具有此屬性。
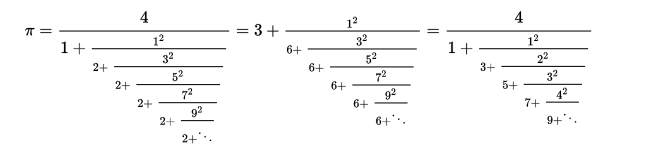
一些不遵循我們規則的漂亮的 pi 連分數表示。
我們將研究看起來像這樣的連分數。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。 透過購買訂閱,您將有助於確保未來繼續產出關於塑造我們今天世界的發現和想法的具有影響力的報道。
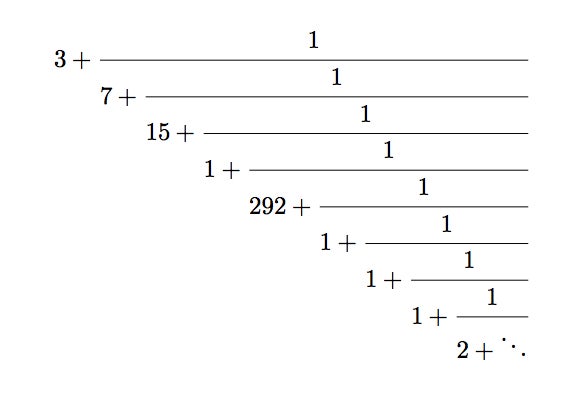
符合我們規則的數字 pi 的連分數表示。
當我們在有限項後截斷連分數時,我們得到所謂的收斂。 數字的連分數表示中的收斂是該數字的最佳有理逼近。 但是我們需要考慮這意味著什麼。 沒有所謂的最接近無理數的有理逼近。 透過增加分數的分母,我們可以根據需要儘可能接近。 截斷數字的十進位制表示是做到這一點的一種方法。 如果我們想獲得更好的數字逼近,我們可以新增更多十進位制項。 因此,任何關於“最佳逼近”的合理想法都是相對的。 它需要考慮分母的大小。
在 A. Khinchin 的關於連分數的經典著作中,他定義了數字“最佳逼近”的兩個概念。 第一個更容易描述:如果分數 c/d 比任何分母較小的數字更接近 a,則分數 c/d 是數字 a 的最佳逼近。 也就是說,對於任何其他分數 p/q,如果 q
所有連分數收斂都是第一類最佳逼近,但它們滿足比這更強的屬性。 基本思想是,如果你讓分母更大,你會在某種程度上付出代價。 這可能是將披薩切成如此小的塊(或者你那樣切時損失的乳酪)的難度,可能是進行計算所需的計算能力,可能只是寫出數字需要多少墨水和精力。 但是是有代價的。 如果我們要在分母上付出這個代價,我們希望我們的最佳逼近真的很好。 我們不只是想要比我們得到的最後一個好的逼近稍微好一點的東西,我們想要一些值得為分母付出代價的東西。
數學條件是這樣的:對於數字 a,如果對於每個其他分母 q
讓我們看看它在 pi 中是如何工作的。 USC 資訊科學研究所的 John Heidemann 有一個包含所有分母高達約 5 千萬的 pi 的最佳有理逼近(第一類)的列表。 數字 3/1、13/4、16/5、19/6 和 22/7 是此列表中的前幾個分數。 13/4 比 3 更接近 pi。 它大約相差 0.1084 而不是 0.1416。 但是,如果我們將差值乘以分母,則 13/4 效果不佳。 我們得到 0.1416×1=0.1416 和 0.1084×4=0.4336,因此 13/4 輸得很慘。 16/5 和 19/6 也是如此。 它們都更接近 pi 一點,但它們不夠接近以彌補它們較大的分母。 因此,13/4、16/5 和 19/6 是第一類最佳逼近,但不是第二類最佳逼近。 但是,當我們到達 22/7 時,情況發生了變化。 它非常接近 pi。 它的差值 0.00126 非常小。 如果我們將其乘以其分母,則得到 0.00126×7=0.00882。 這很容易擊敗 0.1416,因此它是第二類最佳逼近。 它也是 pi 的連分數中的下一個收斂。
我最喜歡的 pi 的連分數收斂是 355/113。 這是一個非常好的逼近。 這是一個連分數的完美示例。 第一類下一個最佳逼近的分母為 16,604。 但它甚至沒有比 355/113 好多少。 我們沒有獲得另一個十進位制數字的精度,但我們必須將分母增加兩位十進位制。 不用了,謝謝。 我們必須增加到分母 33,102* 才能獲得一個新的值得關注的逼近。
下一個逼近 103,993/33,102* 對應於當我們在 292 處截斷 pi 的連分數表示時得到的收斂。 這導致了一個有趣的定性觀察:數字的連分數中的大分母告訴你,你之前得到的收斂確實是一個非常好的逼近。 (記錄在案,“非常好的逼近”不是一個技術術語。)另一方面,小分母意味著先前的收斂不是那麼好。 當你考慮分數是如何工作時,這是有道理的。 大分母意味著我們只需要新增一小片東西就可以更接近我們的目標。
所有連分數收斂都是第二類最佳逼近,因此我們可以將它們視為最佳逼近中的最佳。 這些逼近的分母與僅僅是最佳的逼近(即第一類最佳逼近)之間存在一些有趣的關係。 這有點複雜,但一個有趣的結果是,為了獲得不是第二類最佳逼近的第一類最佳逼近,連分數必須具有除 1 以外的分母。 因此,黃金比例(其連分數僅由 1 組成)只有第二類最佳逼近。 它的所有逼近都是最佳中的最佳。 另一方面,由於所有這些 1,它的最佳逼近是最差的,即使是最佳逼近也可能是最差的。 你甚至可以說黃金比例具有最佳中的最佳中的最差逼近。 或者可能是最佳中的最佳中的最差逼近。
連分數是關於卓越的。 我們不會滿足於平庸的數字逼近(十進位制——呸)甚至僅僅是最佳的逼近。 只有最佳中的最佳才能滿足,只有真正值得寫下來的數字。

保持渴望。
*這些數字在釋出後已更正——我不小心高估了 pi 收斂!