本文發表於《大眾科學》的前部落格網路,僅反映作者的觀點,不一定代表《大眾科學》的觀點
上週日,我寫了我在ScienceOnline上的公共統計會議。今天,我將向您介紹我的另一個會議,動手數學,由Matthew Francis共同主持。如果您參加我們的會議,您可能會帶回家一個屬於您自己的數學曲面。
認識一下艾莉。她看起來可能像一個形狀奇怪的枕頭,但她遠不止於此。

艾莉,一個虧格為 2 的曲面。更多的枕頭應該有虧格。 圖片來源:Evelyn Lamb
關於支援科學新聞業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞業 訂閱。透過購買訂閱,您正在幫助確保未來繼續產出關於塑造我們當今世界的發現和思想的、有影響力的報道。
首先,艾莉是一個虧格為 2 的曲面。她有兩個孔,您可以在這張照片中看得更清楚一些。

艾莉的俯檢視,展示了她確實具有虧格 2 的事實。圖片來源:Evelyn Lamb
曲面在數學中隨處可見,而艾莉是一個非常有趣的曲面,有很多屬性值得探索。例如,她是一個平移曲面。這些曲面是透過在歐幾里得平面上取一個多邊形(在本例中是一塊 L 形的織物),並將相同長度的平行邊粘合(或縫合)在一起而形成的。

一塊 L 形織物,標有標識,使其成為平移曲面。具有相同符號的邊將被縫合在一起。圖片來源:Evelyn Lamb
我將讓 Diana Davis 的 "用舞蹈演繹你的博士論文" 影片用另一種方式解釋它。
雙五邊形上的切割序列,透過舞蹈解釋,來自 Diana Davis,釋出在 Vimeo 上。
在第一個場景中,每當舞者穿過雙五邊形的邊緣之一時,她就會在螢幕的另一部分重新出現,因為我們要想象這個圖形是被粘合起來的,相同顏色的邊被識別出來。
平移曲面本身就很有趣,但當我們研究多邊形上的檯球時,它們也會自然而然地出現。例如,在 L 形的檯球桌上,母球可以採取什麼樣的軌跡?信不信由你,我們可以研究像艾莉這樣的曲面來找出答案。順便說一句,這並非完全是學術性的練習:數學家 Moon Duchin 實際上在南非旅行時偶然發現了一張這樣的 L 形桌子。
一個普通的單孔環面是平移曲面的另一個例子。在這種情況下,多邊形是正方形或矩形。
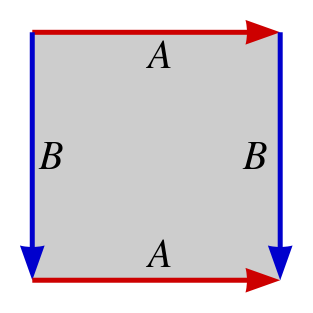
一個正方形,頂部和底部邊標記為“A”,左右邊標記為“B”。透過將具有相同標籤的邊以及對齊的箭頭粘合在一起,製作一個環面。圖片來源:Ilmari Karonen Wikimedia (公共領域)
此動畫顯示了粘合過程

一個正方形捲成一個圓柱體,然後捲成一個環面。圖片來源:LucasVB Wikimedia (公共領域)
我們可以看到,無論我們站在環面的哪個位置,我們周圍的地面都非常平滑。那是因為如果我們看看正方形的角會發生什麼,它們都被識別在一起,但它們周圍正好有 360° 的角度。對於 L 形桌子,情況有點不同。再一次,所有的角都被識別為同一點,但現在我們在這個點周圍的角度遠遠超過 360°。

當進行識別時,所有藍色頂點最終都被識別為同一點。藍色點周圍的綠色弧線幫助我們計算該點周圍的角度量。在這裡我們可以看到,我們有三個圓的角度,1080°。圖片來源:Evelyn Lamb
那個有趣的、難以拍攝的點通常被稱為錐點。我製作艾莉是因為我想擁有一個可觸控的曲面模型,它有點像我研究的那些具有這些有趣的錐點的曲面。她與我的曲面並不完全相同,因為她的皮膚是以無聊的歐幾里得平面而不是我使用的更性感的雙曲平面為模型。但我沒有任何用雙曲鉤針製成的巨大織物片,而且雙曲曲面無論如何也無法完全放入三維空間,所以艾莉是我擁有的最接近的東西。
這使我們回到這篇文章的目的:邀請您來到有趣的數學世界,您可以在我們的動手數學會議上製作和觸控數學。我們將討論我在這裡提到的一些主題:拓撲學、幾何學和動力系統,我們將用織物和紙張製作曲面。Matthew 是一位物理學家,他將介紹這些數學概念在物理學中出現的一些方式。
如果您認為您可能會參加會議,如果您能在wiki上告知我們,我們將不勝感激。我知道這些決定通常是在最後一刻做出的,這完全沒問題。但是,大致瞭解感興趣的人數將有助於我們帶上適量的織物。如果您不能來,您可以在 Twitter 上使用標籤 #HandsOnMath 關注我們。