本文發表於《大眾科學》的前部落格網路,反映作者的觀點,不一定代表《大眾科學》的觀點
去年,莫斯科國立大學的數學家奧爾加·弗羅爾金娜證明了,在三維空間中,你只能放置可數個不相交的莫比烏斯帶。我為《量子雜誌》撰寫了關於她的工作和一些推廣的文章。
如果你還沒有接觸過可數和不可數無限的概念,它們基本上就是它們聽起來的樣子。數學家已經證明並非所有的無限都相等。一種無限是當你開始計數並且永不停止時得到的無限:1、2、3、4、…。這被稱為可數。任何你可以放入一個列表,並具有第一個元素、第二個元素等等的東西都是可數的。另一方面,沒有辦法列出實數,甚至只是 0 和 1 之間的實數。你製作的每個列表都會是不完整的。(要了解原因,請閱讀Yen Duong 的這篇文章。)因此,實數是不可數的。當你體驗過實數的豐富性時,說實話,可數無限聽起來有點微不足道。只有微不足道的無限個莫比烏斯帶可以放入三維空間。
當我在撰寫《量子雜誌》的文章時,佐治亞理工學院的數學家丹·馬加利特告訴了我一個關於平面上字母的類似問題。在平面上放置可數個任意字母並不難,因為你可以將它們放在無限網格上,這是可數的。但是對於某些字母,如果你足夠聰明,你可以在平面上放置不可數多個副本。
關於支援科學新聞
如果你喜歡這篇文章,請考慮透過 訂閱來支援我們屢獲殊榮的新聞報道。透過購買訂閱,你正在幫助確保關於塑造我們當今世界的發現和想法的有影響力的故事的未來。
最簡單的例子是 O。在平面上放置不可數個 O 的方法有很多種,但一種方法是選擇一個半徑為 1 的圓,並考慮適合其中的所有同心圓。沒有兩個具有相同中心和不同半徑的圓會彼此相交,並且存在不可數多個小於 1 的可能半徑,因此我們已經達到了不可數性,我們完成了。
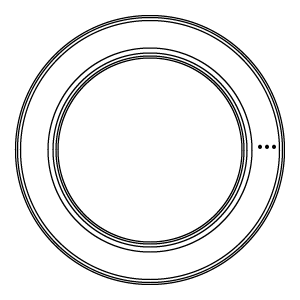
有限數量的巢狀 O。不可數的數量看起來就像一個實心的環。來源:伊芙琳·蘭姆
另一方面,平面上只能放置可數多個 X。因此,無限井字棋遊戲被限制為可數性,因為 X 阻止了 O 的放置。我們如何知道平面上只能放置可數多個 X?首先,我們可以快速驗證我們不能只是將一個 X 放在我們不可數的 O 的每一個裡面,因為 X 會最終彼此相交。但是,正如我在關於莫比烏斯帶的文章中所寫的那樣,這個事實並不意味著沒有更聰明的方法來放置它們。
為了證明不可能在平面上嵌入不可數多個 X,我們利用了有理數的力量。
我學到的關於可數性最重要的課程,至少在能夠證明某些集合是否可數方面,是有理數是可數的。與整數和一些其他可數集合不同,乍一看,有理數是可數的並不明顯。它們太多了!在實數線上的任何微小區間內都有無限多的有理數,至少當我第一次看到這個問題時,我認為有理數一定比整數“更多”。我花了很多時間試圖證明有理數是不可數的,直到另一位學生給出了它們實際上是可數的證明。將我關於可數集合的預設思維方式從整數(它們間隔很好且顯然它們之間有很多空間)轉變為有理數(它們到處混雜,但仍然不知何故比實數少),是我數學發展中的重要一步。證明一個集合是可數的一個好策略是找到一種方法來建立該集合和有理數之間的對應關係,而這正是我們可以用 X 來做的事情。
假設我們在平面上有一堆 X。
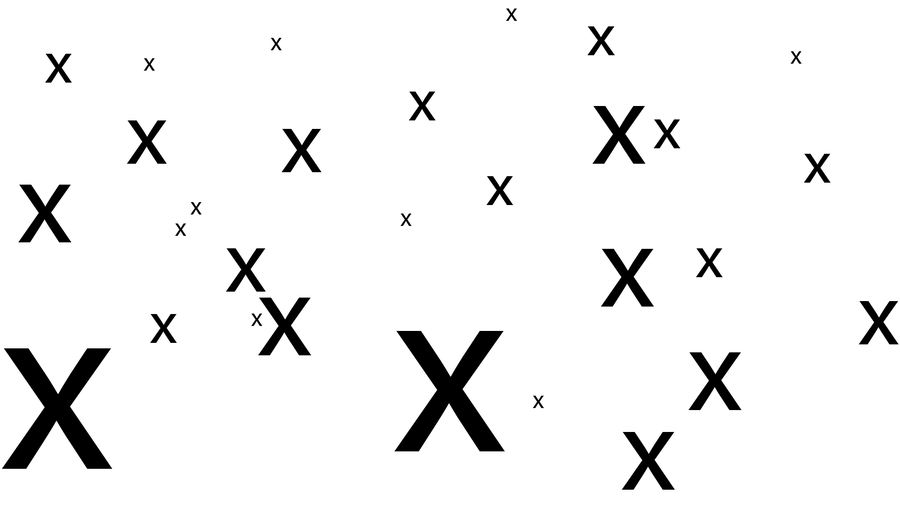
平面上有限數量的 X。嘗試製作無限數量的 X 花費了太長時間。來源:伊芙琳·蘭姆
對於每個 X,我們可以找到一個小的圓,其半徑為有理數,中心具有有理座標,使得 X 在四個點處從圓中伸出。在 X 在圓中建立的每個象限內,我們可以找到一個具有有理座標的點。
.png?w=196)
帶有紫色模板的 X。來源:伊芙琳·蘭姆
所以每個 X 都有 11 個有理數與之關聯:一個用於半徑,每個具有有理座標的點都有兩個。正如比爾·拉塞爾所知,11 有點笨重。幸運的是,作為數學家,我們不需要做任何像將它們戴在手指上之類的實際事情。我們只需要知道它們存在,並且如果我們真的必須這樣做,我們可以列出它們。
當我和他交談時,馬加利特稱圓和有理點為 X 的“模板”。(請注意,每個 X 都有無限數量的潛在模板,因為如果你稍微晃動一個模板,你可以找到另一個有效的模板。)由於這些模板由 11 個有理數定義,因此平面上只有可數多個模板。(我們在這篇文章中沒有實際證明這一點,但如果你願意,你可以自己證明。)因此,如果平面上有不可數多個 X,那麼其中無限多個必須具有相同的模板,因為沒有足夠的不同模板可供使用。最後一塊拼圖是證明任何兩個具有相同模板的不同 X 必然會彼此相交。嚴格證明這一點並非易事,但如果你開始繪製帶有 X 的圓,我認為你可以說服自己。
為了總結一下,唯一的事實是,只有可數多個允許的 X 模板可以在平面上而不相交,這意味著我們只能有可數多個 X。
當我聽到這個證明時,我覺得它很可愛,但它也幫助我發展了一些關於莫比烏斯帶的直覺。弗羅爾金娜的證明不是基於相同的論證,但它讓我更舒服地思考如何甚至處理這樣的問題。
其他字母呢?我們可以在平面上放置不可數多個它們嗎?對於 C 和 D(無襯線,就像我在本文草稿中使用的字型,而不是本文版本中的字型)的答案是肯定的。對於 X 和 Y 的答案是否定的。對於 V 的答案是肯定的。對於 Q 的答案是否定的;它的右下角有一個類似 x 的部分。我開始發展一些理論,即哪些形狀可以在平面上放置不可數多個同類,然後我偶然發現了波士頓大學數學研究生 Sachi Hashimoto 關於此的文章“塗鴉集合論”。當她作為本科生拖延作業時,她開始思考這個問題,並開始思考她看到的一個問題:你可以在平面上嵌入不可數多個 8 字形嗎?“如果你真的在拖延你的作業,你就會從那裡繼續,”她開玩笑說。
她開始塗鴉字母和其他形狀,試圖找出簡單的標準來確定哪些形狀可以在平面上嵌入不可數多次,哪些不能。她和她部落格上的一位評論者也提出了一些猜想,但從未找到確鑿的證據。當我和她談論這個問題時,她告訴我她希望我能一勞永逸地告訴她答案。沒那麼幸運。“時不時地,我會坐下來嘗試證明它,”她說,但作為一名計算數論學家,這並不是她擅長的領域。如果你想閱讀她的猜想並開始自己塗鴉集合論,請檢視她的文章。更新,2019 年 3 月 8 日:Hashimoto 和朋友們繼續研究哪些形狀可以在平面上嵌入不可數多次。檢視她關於此的新文章!
當我在撰寫《量子雜誌》的文章和這篇文章時,我與幾位數學家討論了嵌入不可數多個字母或莫比烏斯帶的問題,很高興看到這個問題在一些非常不同的研究領域的數學家中引起了共鳴。我不確定它對數學家如此廣泛吸引力的確切原因是什麼,但我可以將其推薦為你在與數學家交談時可以使用的開場白。
我認為它吸引人的一點是,它利用了可以被認為是“小”和“大”的概念的數學性質。在不給出嚴格定義的情況下,在某種意義上,X 必須比 O“更大”,因為只有可數多個 X 可以放入平面。同樣,在三維空間中,莫比烏斯帶比圓柱體“更大”。但“大”和“小”的另一個概念是收縮性,即一個空間是否可以在不丟失某些拓撲資訊的情況下縮小到一個點。O 不是可收縮的。這個孔是必不可少的。但是對於 X,你可以將腿推入並得到一個點。再次,在不給出具體定義的情況下,可收縮空間感覺比不可收縮空間“更小”。這個孔可能賦予了一些分量。因此,在字母嵌入的情況下,這些不同的小和大概念以有趣的方式碰撞。
另一種思考這個問題的方式是,它告訴我們的不僅僅是關於物體本身,還包括我們嵌入物體的空間。三維空間對於不可數無限多個莫比烏斯帶來說“太小”了,而平面對於不可數無限多個X來說也太小了。這個問題有如此多的微妙之處和角度,而且看起來似乎只需要幾分鐘的思考就能解決,也許數學家們不斷被它吸引也就不足為奇了。如果你有什麼事情需要拖延(誰沒有呢?),我希望你能享受一下這封塗鴉信帶來的樂趣。
