本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定代表《大眾科學》的觀點
在最近一期我們的播客《我最喜歡的定理》中,我的聯合主持人凱文·克努森和我與卡琳娜·庫爾託進行了交談,她是賓夕法尼亞州立大學的一位數學家,專門研究應用於生物學和神經科學的數學。您可以在這裡或kpknudson.com收聽這一集,那裡也有文字記錄。
庫爾託向我們介紹了佩龍-弗羅貝尼烏斯定理,它來自線性代數領域。正如庫爾託在節目中熱情洋溢地說道,線性代數是數學的支柱之一。它為建模和理解在許多不同背景下出現的方程組提供了一套強大的技術。
關於支援科學新聞業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞業 訂閱。透過購買訂閱,您將幫助確保有關塑造我們當今世界的發現和思想的具有影響力的故事的未來。
線性代數研究的中心物件之一是矩陣。 矩陣是一個數字陣列,但它遠不止於此。這些數字排列成行和列,通常被認為是空間變換的簡寫表示。例如,變換平面的方法之一是取平面中的每個點,寫成 (x,y),並將第一個座標 x 傳送到和 2x+y,第二個座標 y 傳送到 x+y。矩陣
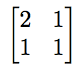
編碼了該變換。
一般來說,從原點發出的射線點可以被矩陣編碼的變換拉伸和旋轉,但在稱為特徵向量的特殊方向上,變換僅限於拉伸或收縮。沒有旋轉。指向該方向的單位長度線段被拉伸或收縮的量就是特徵值。佩龍-弗羅貝尼烏斯定理指出,對於所有條目均為正數的方陣,存在唯一的最大實特徵值,並且其對應的特徵向量具有正 x 和 y 座標。
在與庫爾託交談之前,我隱約記得聽說過佩龍-弗羅貝尼烏斯定理,但最初我並沒有覺得它特別引人注目。我在我的第一堂線性代數課上很早就瞭解到,不要對你在矩陣中看到的數字過於在意。也就是說,你不應該認為僅僅根據矩陣條目的外觀就可以理解矩陣的作用。我認為我早期未能欣賞佩龍-弗羅貝尼烏斯定理的部分原因是,我對一個允許我根據矩陣中的數字瞭解變換的定理有點懷疑。更糟糕的是,沒有多少矩陣的所有條目都是正數,那麼適用於如此排他性矩陣集的定理有什麼意義呢?
庫爾託讓我相信,這個定理比我最初認為的更有用。誠然,沒有理由認為任何任意矩陣都將具有全正條目,但許多應用確實主要處理全正矩陣。表示與人口動態、人口統計學、經濟學和網路搜尋演算法相關的函式的矩陣通常具有全正條目,因此佩龍-弗羅貝尼烏斯定理適用於它們。就目前而言,甚至有一個流行病學模型,Kermack-McKendrick 模型,它使用佩龍-弗羅貝尼烏斯定理。(我提到這個模型不應被解釋為鼓勵大家從事業餘流行病學。)想要更廣泛地瞭解佩龍-弗羅貝尼烏斯定理的許多證明和應用的讀者和聽眾應該檢視一篇名為《佩龍-弗羅貝尼烏斯定理的許多證明和應用》的論文,這篇論文名副其實,《佩龍-弗羅貝尼烏斯定理的許多證明和應用》。
