本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
學習數學最令人沮喪的事情之一是我們編寫教科書和學術期刊文章時,那種掩蓋直覺的方式。我們呈現證明的方式並不是我們得出證明的方式——幾乎感覺就像作者在掩蓋他們的蹤跡。
ε-δ 證明是微積分和分析課程中本科生中出了名的不受歡迎的主題。Delta 和 epsilon,兩個小的正數,構成了嚴謹的微積分證明所依賴的支架,而 δ-ε 證明可能是許多數學學生第一次體驗到我們呈現數學論證方式的人為性的地方。
δ-ε 證明與微積分中的一個基本概念有關:極限的概念。粗略地說,如果函式的輸出可以任意接近 L,只要輸入足夠接近 p,我們就說函式在點 p 處趨近於極限 L。正如數百萬微積分學生多年來一直困惑的那樣,我們嚴格地表述如下:函式 f(x) 當 x 趨近於 p 時,極限為 L,當且僅當對於每個 ε>0,存在一個 δ>0,使得當 x 與 p 的距離在 δ 之內時,f(x) 與 L 的距離在 ε 之內。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞事業 訂閱。透過購買訂閱,您正在幫助確保關於塑造我們當今世界的發現和想法的具有影響力的故事的未來。
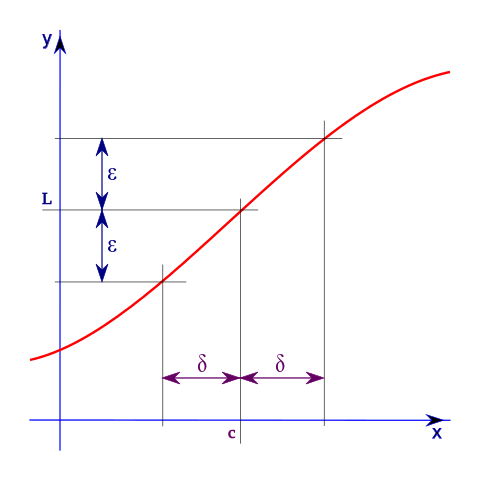
極限的 ε-δ 定義的視覺化表示。當 x 與 c 的距離在 δ 之內時,f(x)=y 與 L 的距離在 ε 之內。圖片:公共領域 (由使用者 HiTe 透過 Wikimedia Commons 提供)。
當您編寫 ε-δ 證明時,尤其是作為本科生,您必須滿足字面意義上的法律要求。您必須證明,無論給定什麼 epsilon,您都可以找出必要的 delta。一個嚴謹的書面證明以“設 epsilon 大於 0”這句話開頭。但是要發現證明,您實際上並不是從 epsilon 開始,而是從 delta 開始。您向輸入 x 新增一個任意的 delta,看看函式的輸出會發生什麼。然後您找出如何使該輸出小於 epsilon。
例如,對於簡單的函式 f(x)=2x+1,證明的內部心智發現和必要的 delta 將會像這樣
|f(x+δ)-f(x)|=|2(x+δ)+1-(2(x)+1)|=|2(δ)|。因此,如果我們想讓 f(x+δ) 與 f(x) 的距離在 ε 之內,我們看到 2(δ) 需要小於或等於 ε。因此我們得出結論,δ=ε/2 就足夠了。
當我們編寫證明時,我們掩蓋了我們的思考過程
設 ε>0。設 δ<ε/2。那麼 |f(x+δ)-f(x)|=|2(x+δ)+1-(2(x)+1)|=|2(δ)|<2(ε/2)=ε。證畢。麥克風掉落。
對於這個函式的情況,不難看出 2 是從哪裡來的,而且證明足夠短,任何懸念很快就結束了。但是,即使在這種簡單的情況下,delta 優先思考和 epsilon 優先寫作之間的視角轉換也很困難。
我模糊地記得第一次在高中微積分課上寫 ε-δ 證明。今天,我可以看看係數和指數,並很快弄清楚 delta 必須用 epsilon 來表示,但在第一個學期,這感覺就像魔術。在我的證明發現過程的開始,我從不知道最終如何使事情奏效。雖然這個過程有點神秘,但我發現弄清楚 delta 必須是什麼,然後寫出證明,掩蓋我的蹤跡,以便我可以在最後得意洋洋地從帽子裡拿出 epsilon,這令人滿意。
如果 Pi Mu Epsilon 尚不存在,Epsilon Delta 將是數學榮譽學會的完美名稱。ε-δ 證明是進入數學證明寫作者秘密社團的入門儀式。