本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
今天晚上最令人興奮的事情是一艘船。在我們住在這裡的兩個月裡,我們公寓隔壁的博物館在門前擺放了一艘巨大的船,作為他們“Aventuriers des mers”展覽的一部分。展覽於週日閉幕,今天他們收拾了船。
雖然我會想念這艘船以及它讓指路變得多麼容易(“沿著塞納河走,直到你看到那艘巨大的船。不,不是在水上。在人行道上。”),但移走這艘船是期待和快樂的源泉。那裡有一臺大型起重機!他們用它吊起了船!這是一個數學和工程學的奇蹟。確保起重機和人行道能夠支撐重量的計算,工人們執行工作的精確度,當然還有現實生活不通勤的重要事實。這場奇觀的協調員需要以正確的順序理解和計劃一切。(點選此處閱讀一篇法語文章,瞭解其前往巴黎的部分旅程,包括部分旅程的影片。)
在所有興奮之後,工作人員用起重機吊起了一艘船,並將其放在平板卡車上。載著船的卡車必須想辦法將船從它停放的公共廣場/人行道運到巴黎的道路上。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和想法的具有影響力的故事。

船停放在卡車上。圖片來源:伊芙琳·蘭姆
我看著船和卡車,以及它們停放的人行道和它們即將行駛的街道之間的障礙物。他們會怎麼做呢?卡車及其裝載物如何在不撞到樹木、建築裝置、城市腳踏車架或戶外雕塑的情況下到達道路?我透過思考卡克亞針問題來緩解我的焦慮。
我不知道以這個問題命名的數學家卡克亞崇一是否是一個特別寧靜的人,但卡克亞針問題給了我寧靜。這個問題詢問的是在二維平面內旋轉線段(或針)所需的最小面積。(假設針的寬度為零。)
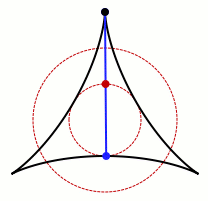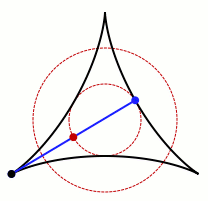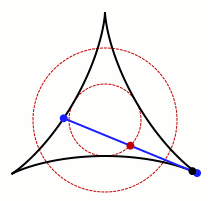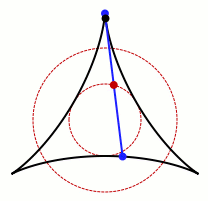
允許卡克亞針旋轉的集合的動畫。圖片來源:Claudio Rocchini Wikimedia (CC BY-SA 3.0)
不難看出,這個過程在圓形、正方形和等邊三角形中是可行的。上面的gif也表明,它也適用於非凸形狀,即向內彎曲的形狀。
卡克亞在1917年提出了這個問題,阿布拉姆·薩莫伊洛維奇·貝西科維奇在1928年解決了這個問題,表明不存在大於0的最小面積。如果你轉動得足夠慢,在足夠長的長度上轉動,你將能夠使面積小於你想要的任何正數。你可以用鉛筆徒手玩卡克亞問題。
我求助於卡克亞問題來尋求安慰,不僅當我在觀看平板卡車運載巨型船進行n點轉彎時,而且當我在駕駛我的汽車並且需要在狹窄的空間內掉頭時。我將卡克亞問題視為駕駛的“如果你能進去,你就能出來”定理,儘管我意識到它們並不完全相同。卡克亞的問題不在乎你是如何到達那裡的,它還假設你的汽車是無限薄的,並且你有無限的長度可以利用。駕駛時情況並非如此;儘管如此,我還是允許它讓我安心。至少,它提醒我要利用我擁有的空間,並且在轉彎時再增加一個點並不丟人。
理論與實踐之間的差距有時感覺很大,卡克亞問題也不例外。但是,正如一個在數學考試中被要求“證明或找到反例”的學生可能會告訴你的那樣,知道一個問題是可解的,可能是取得進展和決定將你的汽車遺棄在狹窄的停車場或死衚衕的盡頭之間的區別。因為我知道卡克亞針問題說是有足夠的空間,所以我將繼續慢慢移動自己,最終會走出去。我不知道移動船的平板卡車司機是否求助於卡克亞針問題來獲得勇氣,但船最終安然無恙地駛出了,並駛入了巴黎的夜空。
