本文發表於《大眾科學》的前部落格網路,反映作者的觀點,不一定代表《大眾科學》的觀點
彼得·舒爾茨是 8 月初在國際數學家大會上獲得表彰的四位菲爾茲獎得主之一,他研究代數幾何。該領域的一個核心問題是多項式方程何時存在整數或有理解。例如,方程 x^2+y^2+z^2=1,它在三維空間中定義了一個球體,有解 (3/13, 4/13, 12/13)。
在他的菲爾茲獎講座中,舒爾茨談到了他在 p 進幾何方面的工作。(您可以閱讀他為配合講座而撰寫的綜述文章這裡,但坦率地說,如果您能讀懂那篇文章,您就不需要閱讀我的帖子了,因為您對 p 進數的理解已經遠超我了。)p 進數是一種替代的數系,有時比實數更適合解決代數幾何和數論中的問題。
有幾條道路可以通往 p 進數。其中一種方法是從絕對值開始。我們習慣於標準絕對值,它衡量一個數到 0 的距離。如果一個數大於 0,其絕對值就是它本身,如果一個數小於 0,其絕對值就是它本身的相反數。因此 |1|=1 且 |-1|=1。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您將幫助確保未來有關當今塑造我們世界的發現和想法的具有影響力的故事。
我們可以引入一種不同的方法來衡量數的大小,即基於它與數 p 的關係。如果您上過一些高等數學課,p 可能讓您感覺有點奇怪。數學家通常在談論素數時使用字母 p,並且在本文的其餘部分中,我們將假設 p 是素數。當談論特定 p 的 p 進數時,數學家會用數字本身代替 p,因此我們談論 2 進數、3 進數、29 進數、314159 進數,您明白了。(是的,314159 是素數。即使我對 π 日嗤之以鼻的心也會為此微微顫動。)
一個數的 p 進絕對值是能整除它的最大 p 的冪的倒數。在這種情況下,一個具體的例子可以使這個複雜的概念更容易理解。讓我們先看看 3 進數。數字 4 不能被 3 的任何正冪整除。它等於 30x4。這意味著 1 是能整除 4 的最大 p 的冪,使 4 的 p 進絕對值等於 1/1,或 1。數字 6 有點更有趣。它等於 31x2,使其絕對值等於 1/3。54 的 3 進絕對值是 1/27,因為 27 是能整除 54 的最大 3 的冪。非常大的 3 的冪的倍數具有非常小的 p 進絕對值。
3Blue1Brown 還在這個影片中,用 2 進數的例子解釋了 p 進數的概念。
p 進絕對值有一些有趣的性質,而通常的絕對值沒有。例如,有很多數字具有相同的絕對值。數字 1、2、4、5、7、8 和其他無限的數字串都具有 3 進絕對值 1。數字 3、6、12、15、21、24 等都具有絕對值 1/3。我們通常的絕對值最多隻允許有兩個數字具有相同的絕對值。此外,數字不是能夠具有連續範圍的絕對值,而是具有一組離散的選擇。它們有無限多個,但任何數字的大小必須是 p 的冪。因此,沒有數字的 3 進絕對值為 1/2 或 7。我們正在以一種奇怪而不同的方式思考數字。
p 進絕對值給我們提供了一種新的方式來衡量兩個數字之間的距離。兩個數字 x 和 y 之間的 p 進距離是數字 x-y 的 p 進絕對值。因此,回到 3 進數,這意味著如果兩個數字的差是 3 的大冪,則它們彼此更接近。數字 1 和 4 的差是 3,因此它們之間的 3 進距離是 1/3。但是數字 1 和 19 的 3 進距離是 1/9 (18=32x2),而 1 和 82 的 3 進距離是 1/81。數字 11 和 29 的差是 18,因此它們的 3 進距離是 1/9。
如果您使用過模算術,這可能會讓您感到有點熟悉。在模運算中,或者說模 n,您只關心一個數字與 n 的倍數有多接近。數字 2、9 和 93 模 7 等價,因為它們都比 7 的倍數多 2。在某種程度上,p 進距離給人的感覺是您同時關心所有冪 pk 的模 pk 的數字。
嘗試理解新的距離度量方法的一種方法是嘗試弄清楚在這種距離中什麼與什麼接近。在 3 進度量中,正整數彼此之間的最大距離為 1 個單位,因此我們可以將它們都視為生活在這個有界的圓圈中。
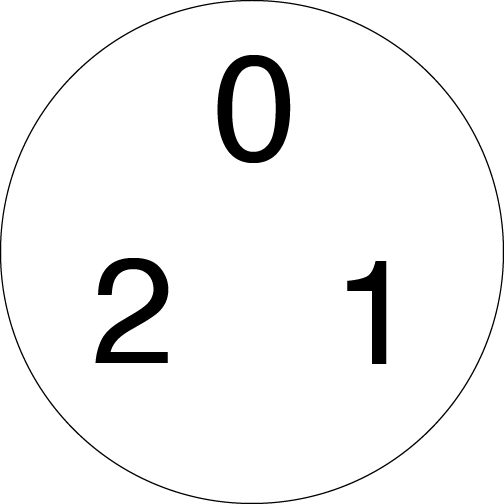
數字 0、1 和 2 位於 3 進數氣泡中。所有其他正整數也位於此圓圈中,但如果我們僅從這些數字開始,我們可以以一種簡潔的方式看到結構的出現。 來源:伊芙琳·蘭姆
讓我們將這個圓圈視為意味著圓圈內的任何東西與任何其他東西的距離最多為 1。現在我那裡只有數字 1、2 和 3,但是所有大於等於 0 的整數都在那裡,因為它們彼此之間的距離最多為 1。
現在我們可以新增另一層。數字 3 距離數字 0 只有 1/3,數字 4 距離 1 只有 1/3,而 5 距離 2 只有 1/3。我們可以將這些數字新增到較小的圓圈中。如果兩個數字在同一個較小的圓圈中,則它們彼此之間的距離最多為 1/3。
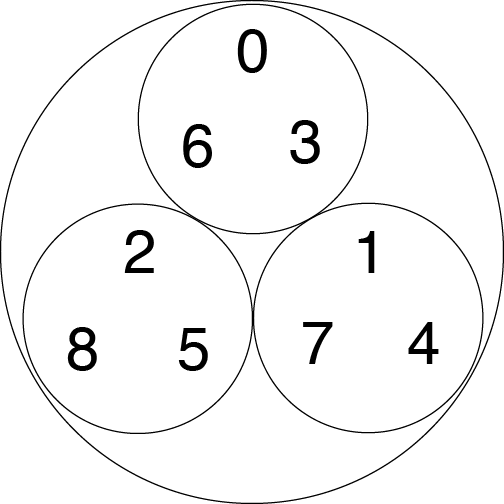
以 3 進數排列的數字 0 到 8。例如,數字 0、3 和 6 彼此之間的距離都為 1/3,因此它們在同一個小圓圈中。來源:伊芙琳·蘭姆
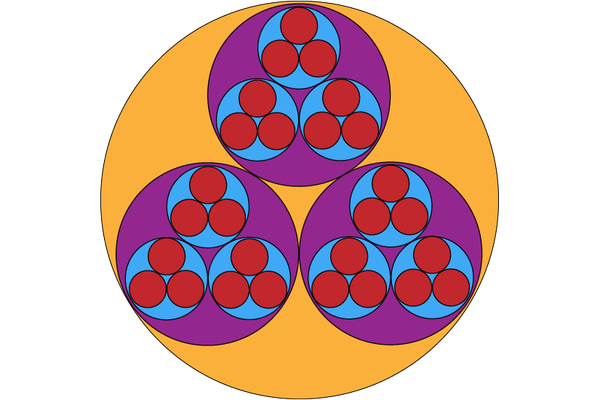
我將繪製此過程的另一層,但我們可以永遠繼續下去,產生一個類似於謝爾賓斯基三角形的美麗分形圖案。兩個數字之間的距離是包含它們的最小圓圈的大小。
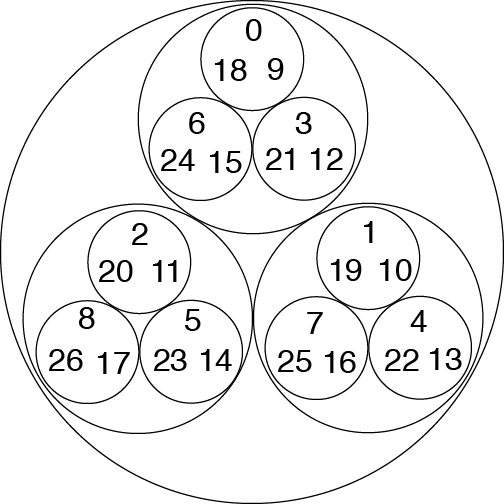
基於數字 0-26 彼此之間的 3 進距離的表示。來源:伊芙琳·蘭姆
哇!這有很多工作要做,而且我們甚至還沒有超出正整數的範圍。但是 p 進數不會止步於此!您可以將 p 進絕對值和距離函式擴充套件到所有有理數。
一個數的 p 進絕對值基本上衡量它的 p-ishness。p-ishness 越高,數字的絕對值就越小。因此,為了將其擴充套件到分數,如果分數的分子可以被 p 的冪整除,我們希望 p 進絕對值很小。為了平衡,如果分數的分母可以被 p 的冪整除,則該數具有較大的 p 進絕對值。(我們假設分數以最簡形式書寫,因為您為什麼要以其他方式書寫?)數字 1/2 實際上與 3 無關,因此其 3 進絕對值為 1。數字 3/4 的分子中有 3,因此其 p 進絕對值是 1/3,就像 3 本身的 p 進絕對值一樣。數字 1/3、2/3 和 5/6 的 3 進絕對值都是 3。數字 1/9、7/9 和 2/63 的 3 進絕對值都是 9,您可以看到規律。非常大的 3 的冪具有非常小的 3 進絕對值,而非常大的 1/3 的冪具有非常大的 3 進絕對值。我們可以想象向上面的 p 進數圖新增數字。我不會這樣做,但我們可以開始弄清楚在哪裡將一些分數新增到上面的 p 進數圖中。數字 1/2 在 3 進數中與數字 5 非常“接近”,因為 5-1/2,4 1/2,可以寫成 9/2,並且分母中有一個 3 的冪。
這篇文章已經很長了,我們甚至還沒有涉及到如何以 p 進數書寫數字!如果您好奇,您必須在其他地方檢視。您可以從 Cut-the-Knot 的這兩個頁面開始。這些p 進展開非常酷,在概念上與以 p 為底而不是以 10 為底書寫數字相關,但又有所不同。關鍵是,我們得到了一些奇怪的東西,例如,在 3 進數中,無限字串 ...222222(左邊是無限的!多麼令人興奮!)是數字 -1 的表示形式,無限字串 ...11111112 表示 1/2,以及其他奇怪的樂趣。在弄清楚如何以 p 進數表示所有有理數以及如何使用它們進行算術運算之後,我們發現缺少了一些東西。
使用數字之間的常用距離,我們也會覺得有理數是不完備的。我們可以想到一些有理數序列,當它們平方時,會越來越接近 2,但是沒有哪個有理數的平方是 2。我們可以找到一些有理數,它們越來越接近直徑為 1 的圓的周長,但是數字 π 不是有理數。我們可以把實數看作當我們加入某些有理數序列(稱為柯西序列)的極限,但最終並沒有得到有理數本身時所得到的東西。這種技術的術語是完備化。實數集是有理數的完備化。我們可以對 p 進距離函式做同樣的事情。存在一些有理數序列,它們在 p 進世界中並不會最終收斂到一個有理數。我們可以加入“缺失的”數字,以獲得完整的 p 進數集。
你現在可能會有一個問題:“我為什麼要這樣做?!”構造 p 進數並非易事或直觀。我聽過一些擁有數學博士學位的人說,如果他們遇到 p 進數,他們總是不得不去查閱它的定義。我就是這樣。肯定會有一些回報!
這個問題非常合理,是的,p 進數確實有很好的回報。首先,它們讓我在 Twitter 上開了這個玩笑
有理數的最佳完備化,排名
10. 你
9. 不能
8. 排名
7. 它們
6. 它們是
5. 全部
4. 有用的
3. 並且
2. 美麗的
1. 實數
— Evelyn Lamb (@evelynjlamb) 2018 年 8 月 27 日
(有理數的完備化有無限多個,但它們只有兩種型別:實數和所有素數 p 的 p 進數。我非常喜歡 p 進數,但思考 p 進數就像拼命地游泳。在進行完 p 進數鍛鍊後,能沉浸在溫暖平靜的實數浴缸中是一種解脫。不過,有些數學家不同意這種觀點。在《Quanta Magazine》的一篇文章中,引用了 Scholze 的話,他說:“現在我發現實數比 p 進數要困惑得多。我已經習慣了它們,現在實數感覺非常奇怪。”)
p 進數不僅僅是用來在 Twitter 梗上晚到幾個月。其中一個最重要的應用是解決我在文章開頭提到的問題:確定特定方程是否有有理數解。如果一個多項式方程在考慮實數時有有理數解,那麼它對於所有數字 p 也都有 p 進數解。這意味著如果你找到一個方程沒有 p 進數解的 p,你就自動排除了有理數解。因此,如果可以透過某些 p 的 p 進數來輕鬆處理某個特定方程,那你可能很幸運。但是,總的來說,你可以用 p 進數代替實數做任何你想要的數字方面的事情,然後看看會發生什麼。你可以使用 p 進數構建微積分的版本。你可以使用 p 進數構建複雜的代數和幾何結構。p 進數是 Scholze 開創性工作的重要組成部分“完美空間”的根源。一些研究人員正在研究 p 進數是否能在物理學中產生成果。
閱讀更多我喜歡的空間: 康托爾集 胖康托爾集 拓撲學家的正弦曲線 康托爾的漏帳篷 無限耳環 兩條原點的直線 有兩個房間的房子 法諾平面 環面 三維環面 莫比烏斯帶 長直線 空間填充曲線 沃利斯篩子 沿著一條縫粘合的兩個環面 空集 門格海綿 四個霍普夫鏈環的連通和 波羅密環 謝爾賓斯基三角形 單位正方形上的字典序 SNCF 度量 曼德勃羅集 法圖煎餅 偽球面 杜阿迪兔子 龐加萊同調球面 科瓦列夫斯卡婭陀螺 一個 6 孔環面 實射影平面 一維球面 尼斯湖水怪 科赫雪花 雙圓柱體 懸鏈面 SO(3) 偽菱形二十面體 莫澤紡錘 阿涅西的女巫 安託萬項鍊 n 個圓的束