本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定代表《大眾科學》的觀點。
當我高中英語課學到轉喻和提喻這兩個詞時,我被它們深深吸引了。(當然,並沒有著迷到我能夠始終記住哪個是哪個的地步。也許這篇文章會改變這一點。我現在有了一個方便的新助記符,雖然對其他人幾乎沒有幫助:轉喻用於矩陣。)
提喻是一種修辭手法,用部分代表整體,反之亦然。“全體船員到甲板上”是一種提喻:這些手大概是連線在整個人身上的,除非你正在看一部關於船的恐怖電影。“芝加哥贏得了世界大賽”用一個更大的整體——一個城市——代替了一個部分——他們的棒球隊之一——儘管看到芝加哥慶祝,也許整個城市真的都贏了。但話又說回來,芝加哥是一個包含許多除了人之外的東西的地方,而慶祝世界大賽的人,嗯,是人,所以我猜這仍然是提喻。
轉喻是用一個相關的詞代替另一個詞。“香檳”用“起泡的”代替可能是轉喻,但也可能是提喻,因為氣泡是在香檳裡。這一切都非常令人困惑。更重要的是,提喻是轉喻的一種,所以用轉喻這個詞來表示所有這些更安全。(另一方面,用提喻來表示所有轉喻是提喻,這非常詩意。)
關於支援科學新聞
如果您喜歡這篇文章,請考慮訂閱來支援我們屢獲殊榮的新聞報道。 透過購買訂閱,您正在幫助確保關於塑造我們當今世界的發現和想法的具有影響力的故事的未來。 暫時拋開詞語用法的複雜性,我一直在思考矩陣的數學轉喻。 當我在二月份寫關於空間SO(3)時,我注意到矩陣是一個數字陣列,這個描述極大地低估了它的效用。(這就像把塞雷娜·威廉姆斯描述為脊索動物門的一員:沒錯,但真的不是重點。)
沒錯:矩陣是一個數字陣列。但正是你對這些數字所做的事情才讓它變得特別。矩陣在數學中最常用於表示線性變換。我們大多數人在早期教育中就學習了簡單的線性變換。方程y=4x就是線性變換的一個例子。它碰巧是一個輸入一個數字x,輸出另一個數字y的變換。線性變換必須保持加法和標量乘法:如果向輸入新增某個東西,則輸出應按比例變化;如果將輸入乘以某個特定量,則輸出應乘以該量。
像y=4x這樣的線性變換,那些輸入一個變數並輸出一個變數的變換,坦率地說,有點無聊。它們看起來都和y=4x一樣,除了4的位置可能有一個不同的數字。(4 只是我選擇的一個隨機數。)但是線性變換可以輸入比一個變數多得多的變數,並輸出多得多的變數。
例如,假設我們要定義一個輸入兩個變數並輸出兩個變數的變換。假設我們想要輸入座標(x,y)並得到數字(2x+y,x+y)。我們可以用類似的方式定義許多不同的函式。存在將(x,y)轉換為(5x-3y,πx+y)的函式,將(x,y)轉換為(.3x,2y)的函式,以及大量的其他函式。數學家們開發了矩陣來處理這些函式。第一個函式可以用矩陣
表示,下一個用矩陣
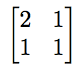
表示,下一個用
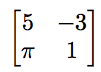
表示。
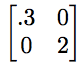
我們可以用它們來表示輸入和輸出變數數量不同的函式。將(x,y,z)轉換為(z-y,x+2y)的函式得到矩陣
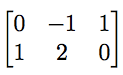
熟悉將矩陣應用於向量需要一些練習,而熟悉矩陣相乘來表示函式的組合(先執行一個函式,然後在第一個函式的輸出上執行另一個函式)則需要更多練習,但一旦你做到了,它就是一個強大的工具。
作為一種工具,矩陣非常強大,以至於很容易忘記它是函式的表示,而不是函式本身。矩陣確實只是數字陣列,但我想在這種情況下,大多數數學家都是轉喻主義者。(轉喻者?轉喻主義者?)我們認為矩陣是函式本身,很容易忽略它只是一個符號。矩陣甚至不必編碼線性變換。它們也在數學的其他領域中使用,將我們的定義限制為線性變換可能會忽略其他應用(儘管在我看來,矩陣作為一種表示線性變換的方式的價值遠遠超過它們的任何其他用途)。
在釋出關於矩陣就像塞雷娜·威廉姆斯的推文後,我很高興在 Twitter 上就矩陣、線性變換和線性代數的教學展開了熱烈的討論。有些人很高興他們將線性變換與矩陣分開學習,有些人則很享受最終理解他們一直在努力的矩陣是更大的圖景的一部分的“頓悟”。我認為在某個時候,人們必須進行一定程度的轉喻才能達到他們可以舒適地使用矩陣作為線性變換並在該上下文中釋放其全部能力的地步,但我們偶爾記住矩陣是轉喻可能是好事。
