本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
當你看著它時,它就靜止不動,保持恆定。但如果你在康託集中的某個點上稍稍轉過身,這個函式就會以令人難以置信的速度增長。

它不是哭泣天使,它是魔鬼的階梯,或者,如果你不那麼異想天開,就是康託函式。我第一次看到康託集被充分運用是在定義這個函式時,它是分析學或微積分學中常見的反例,而不是拓撲學。(如果你以前沒見過康託集,請檢視我上週關於它的帖子。)
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道: 訂閱。透過購買訂閱,您正在幫助確保關於塑造我們當今世界的發現和思想的具有影響力的故事能夠繼續下去。
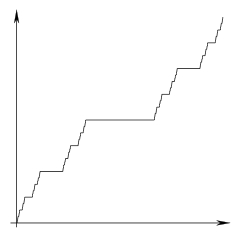
康託函式。圖片來源:Theon,維基共享資源。CC BY-SA 3.0
就像康託集本身一樣,有幾種不同的方式來思考康託函式。第一種是像構建康託集一樣,迭代地構建它。最終,我們希望在整個區間 [0,1] 上定義這個函式。我們將從構建康託集時移除的第一個區間開始,並宣告函式在該區間上的值為 1/2。因此,如果 x 在 1/3 和 2/3 之間,則 f(x)=1/2。接下來,我們將定義它在接下來移除的兩個區間上的行為。我們將區間 (1/9,2/9) 傳送到 1/4,將 (7/9,8/9) 傳送到 3/4。我們繼續遵循這種模式:每個為構成康託集而移除的區間都會被髮送到某個分母為 2 的冪的分數。其餘的點只是“填補空白”。
這個動圖很好地展示了這個過程。
如果你願意用不同的進位制來思考,還有另一種非常巧妙的方式來描述康託函式。首先,像描述康託集一樣,你用 3 進製表示 0 到 1 之間的所有數字。如果一個數字包含 1,則在第一個 1 處截斷它,或者等效地,用 0 替換所有後續數字。如果數字不包含 1,則暫時保持不變。無論哪種方式,下一步都是將數字中的所有 2 替換為 1,並以 2 進位制而不是 3 進位制解釋結果。例如,數字 1/2 在 3 進制中寫為 0.111...。我們在第一個 1 處截斷它得到 0.1 或 0.100...,然後我們以 2 進位制解釋該數字。結果我們再次得到 1/2。
如果你記得康託集是可以以不含 1 的 3 進制書寫的數字集合,那麼有和沒有 1 的數字應該區別對待似乎是合理的。當我們從第一個 1 處截斷時,我們確保函式對於 1/3 和 2/3 之間的每個數字都取相同的值,這是我們在迭代構建康託集時移除的第一個區間。
當我們定義康託集本身時,我們必須小心以 1 結尾的有理數。令人驚訝的是,對於康託函式,我們不必小心!以 1 結尾的有理數可以重寫為以無限個 2 結尾:1/3,或 0.1,與 0.02222… 相同,等等。(如果這看起來很奇怪,請記住 0.9999…=1。3 進制中的數字 2 的作用類似於 10 進制中的數字 9。)
你可能會認為這種歧義會成為一個問題,因為康託函式在某一點的值取決於該點是否包含 1。讓我們看看 1/3,即 0.1 或 0.02222…。如果我們把這個數字看作 0.1,康託函式的定義告訴我們函式值應該是 0.1 (2 進位制),或 1/2。如果我們把這個數字看作 0.02222…,我們應該把所有的 2 都改成 1,得到 0.01111…。當我們以 2 進位制解釋這個數字時,我們也得到 1/2。這在一般情況下都適用。所以我們可以用任何我們想要的方式寫出康託集的端點,並得到相同的數字。
該函式在任何地方都是連續的,這意味著它在整個區間 [0,1] 上都有定義,並且不會跳躍。(我通常透過說一個函式是連續的,如果你可以在不將筆從紙上抬起的情況下繪製其圖形,來直觀地描述連續性,但如果我們考慮迭代地構建這個函式,這就不太好用了。)連續性並不太神奇。導數才是事情變得有趣的地方,康託函式成為了一個很好的反例。
在微積分中,一個函式在特定點是可微的,或具有導數,如果你可以在該點為其圖形繪製切線。如果你學過微積分,你可能還記得你的老師對微積分基本定理的美妙之處感到有點陶醉。(或者只是我?)該定理表明,在某些條件下,求曲線下面積(積分)和求曲線斜率(微分)是“逆”運算。具體來說,微積分基本定理的一部分指出,對於“足夠好”的函式,函式導數的積分告訴你函式在兩個端點的值之差。
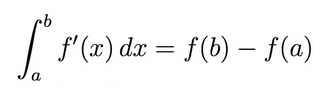
康託函式幫助我們理解“足夠好”意味著什麼。
在康託集之外的每個點,康託函式都是平坦的,因此很容易在該點為圖形繪製切線。(那裡的導數為 0。)正如我們上週看到的那樣,康託集之外的點集總長度為 1,因此從技術意義上講,該函式的導數“幾乎處處”為 0。用哭泣天使的比喻來說,這意味著如果我們碰巧在任何時間點看它一眼,它很可能完全靜止不動,因為我們可能會選擇一個不在康託集中的點。在康託集的點上,情況就不同了。表現最好的康託集點具有“無限”導數,或垂直切線。更病態的點甚至沒有這個。(有關康託函式究竟有多不可微的更技術性討論,請檢視這篇Richard Darst 於 1993 年發表的論文 (pdf)。)
在數學中,“幾乎處處”對於很多事情來說都足夠好了。人們可能會很自然地認為,如果一個函式在任何地方都是連續的,並且幾乎處處可微,那麼它應該足夠好,以至於函式導數的積分可以告訴我們一些關於函式本身的有意義的資訊。但是康託函式向我們表明,這些標準是不充分的。導數幾乎處處為 0,因此導數的積分也是 0,但起始值為 0,結束值為 1。在我們沒注意的時候,它悄悄地上升了。

