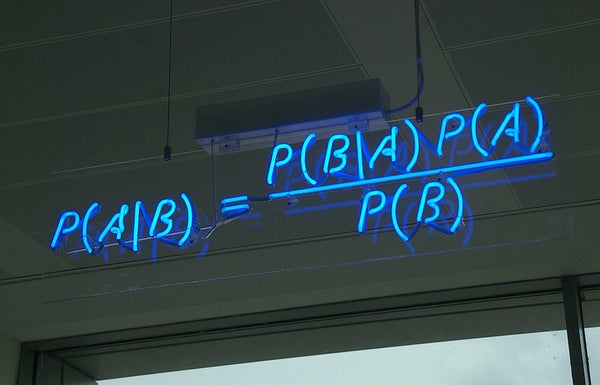本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
在我們最近一期的播客“我最喜歡的定理”中,我的聯合主持人凱文·努森和我與蘇菲·卡爾進行了交談,她是一位顧問,正如她所描述的那樣,“在數字中尋找模式”。她也是大型網際網路數學競賽評選出的“世界上最有趣的數學家”,這是一個由 Aperiodical 在去年夏天主辦的有趣比賽。(今年一月,我們邀請了2018年“世界上最有趣的數學家”尼拉·張伯倫作為節目的嘉賓。)
您可以在這裡收聽,也可以訪問kpknudson.com,那裡也有文字稿。
關於支援科學新聞業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您將有助於確保未來能夠繼續講述關於發現和塑造我們當今世界的想法的具有影響力的故事。
我很高興聽到卡爾最喜歡的定理是貝葉斯定理,因為我一直覺得我對這個定理的理解不夠深入。貝葉斯定理是關於條件機率的陳述——在已知其他條件的情況下,事件發生的機率。一個經典例子是,假設您的檢測結果呈陽性,那麼您患有該疾病的機率。答案取決於該疾病在人群中的流行程度以及檢測的準確性——也就是說,如果您患有該疾病,檢測結果呈陽性的可能性有多大,以及如果您沒有患病,檢測結果呈陽性的可能性有多大。如果一種疾病很罕見,並且該檢測會將大量健康人誤診為患有該疾病,那麼即使您的檢測結果呈陽性,您也可能不太可能患有該疾病。
貝葉斯定理量化了這些機率。它也構成了貝葉斯統計的基礎,貝葉斯統計是統計學的兩個主要分支之一。(另一個是頻率主義。)對貝葉斯統計和頻率主義統計的複雜性和相對優點的完整解釋比我想在這裡討論的要複雜得多,但它們來自關於機率和不確定性含義的兩種不同哲學,統計學家可以使用這兩種方法來開發幫助使用這些技術的人理解世界的技術。對於卡爾來說,貝葉斯定理和貝葉斯推斷感覺像是人類透過與世界互動來學習的直覺方式的自然延伸。在貝葉斯推斷中,您不斷根據先前的信念和新的證據更新您的信念,使用諸如貝葉斯定理之類的工具。
在與卡爾討論了貝葉斯定理之後,我仍然對貝葉斯定理的熱情不高,但這一集確實幫助我更新了我的先驗。再多一些積極的體驗,我也可能成為貝葉斯愛好者。