本文發表於《大眾科學》的前部落格網路,僅反映作者的觀點,不一定反映《大眾科學》的觀點
注意:巧合的是,這篇文章發表後不久,就傳出了關於 Facebook 令人不安的、可能非法的做法的新聞,即允許企業根據“種族親和力”將使用者排除在某些廣告之外。我很樂意您閱讀我這篇關於使用 Facebook 玩轉拉姆齊理論的愚蠢博文,但如果您今天只打算閱讀一篇與 Facebook 相關的文章,那麼Pro Publica 揭露這種令人震驚的做法的文章 絕對更重要。
幾乎每天早上,我都會檢視 Facebook,看看我的哪些朋友在慶祝生日。我很少在網上祝他們生日快樂,因為這似乎太沒有人情味了。(具有諷刺意味的是,在 Facebook 上收到這麼多朋友的生日祝福總是讓我感覺很棒,即使是那些我不常聯絡的朋友也是如此。我是否自相矛盾?好吧,那我就是自相矛盾。我很大,我包含了很多。)但我喜歡以一點拉姆齊理論開始我的一天:如果所有同一天生日的朋友都互相認識,或者他們都不認識彼此,我會感到興奮。
拉姆齊理論在維基百科上的定義晦澀難懂,是“數學的一個分支,研究秩序必須出現的條件”。這相當有詩意,而且我認為如果你已經知道拉姆齊理論是什麼,這似乎是一個很好的定義。但也許一個例子會更清楚地說明“秩序必須出現的條件”是什麼意思。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您將有助於確保有關塑造我們當今世界的發現和思想的具有影響力的故事的未來。
拉姆齊理論的常用例子通常被稱為朋友與陌生人定理,這也是我進行 Facebook 生日檢查的靈感來源:如果一個聚會上至少有六個人,那麼一定有一組三個人都互相認識,或者三個人都是陌生人。數學家西蒙·潘佩納在 Numberphile 上對此進行了解釋,如果您想了解更多關於為什麼這是真的的細節。另一方面,如果你的聚會上只有五個人,你就不能保證這一點。這個紅色五邊形內的藍色星星就是證明。
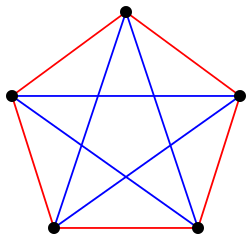
假設五邊形的頂點是聚會上的五個人,如果他們互相認識,則用藍線連線,如果他們是陌生人,則用紅線連線。我們可以看到,每個三角形要麼有兩條紅色邊和一條藍色邊,要麼有兩條藍色邊和一條紅色邊。
來源:Richtom80 Wikimedia (CC BY-SA 3.0)
朋友與陌生人定理與必須出現的秩序有什麼關係?這裡的秩序是三個都互相認識或都是陌生人的人,而“必須出現”是指聚會上的人數達到六個時,朋友或陌生人的三角形是強制性的。
研究拉姆齊理論的人會說,拉姆齊數 R(3,3)=6。拉姆齊數 R(m,n) 是你必須邀請參加聚會的最小人數,以保證m 個人都互相認識或 n 個人都是陌生人。(數字 m 和 n 不必相同。)如果你想確保你能找到 3 個共同的朋友或 4 個共同的陌生人,你將要求拉姆齊數 R(3,4),它恰好是 9。
我的早晨 Facebook 儀式讓我思考,關於我的 Facebook 好友,我可以提出哪些有趣的拉姆齊理論問題。生日這件事為正常的拉姆齊數問題增加了一層額外的結構。現在,我不再將我所有的朋友視為一個大群體,而是將他們分成 366 個較小的群體,每個群體對應一個可能的生日。(是的,我有閏日出生的朋友。)我好奇的問題是,是否需要任何相同顏色的節點成為一個互相認識的朋友或互相陌生的陌生人群體。我知道這對於我的個人朋友群體來說是正確的,但對於任何擁有與我相同數量的朋友的人來說,這是否也必須是正確的?或者更具體地說,我知道我一年中有幾天有六個朋友是互相認識的朋友或互相陌生的陌生人。對於任何擁有與我相同數量的 Facebook 好友的人來說,這是否是必要的?為了使這種情況必須成立,最少需要多少 Facebook 好友?
當我思考了一段時間後,我意識到生日分組是一個轉移注意力的東西。一年中的任何一天都可能在 0 到我所有朋友的生日之間。對於我的一些問題,你必須檢視生日都在同一天的邊緣情況,而對於另一些問題,你必須檢視生日最大程度分散的邊緣情況。無論哪種方式,你都不會得到比不按生日分組的問題更有趣或更困難的問題。好吧,有得必有失。
重點是什麼?不僅僅是為了向你丟擲一些拉姆齊理論的趣聞,雖然我確實喜歡這些趣聞。我只是想分享一種小方法,即一點數學在一定程度上豐富了我的生活。關於數學,特別是數學教育的討論很多,都集中在為什麼數學對工作或日常生活有用。我們也看到了相當多的關於數學之美的神秘主義。這些都很好,但我只是喜歡把數學作為另一種看待世界的視角。我略微瞭解拉姆齊理論的事實意味著,大多數早晨(有些日子我的 Facebook 朋友都沒有生日),當我檢視那裡是否有有趣的朋友或陌生人配置時,我會多花幾秒鐘思考一些過生日的朋友。到目前為止,我注意到的最大的有趣群體是我認識的 3 月 5 日出生的六個互相陌生的陌生人。我正在祈禱有一天我能達到七個!