本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
上個月,我得知印度數學家Sharadchandra Shankar Shrikhande去世,享年102歲。這個名字聽起來很耳熟,因為不久前我瞭解了“格雷科-拉丁方陣”,這是他最著名的數學構造。
要理解Shrikhande的工作,我們必須追溯到幾個世紀前,傳奇瑞士數學家萊昂哈德·尤拉(Leonhard Euler,1707-1783),他在去世前不久寫到了這個問題。(這是他關於此論文的英文翻譯。)拉丁方陣是一個n×n陣列中n個符號的排列,使得每個符號在每行每列中出現一次。(數獨是9×9的拉丁方陣,但也滿足額外的要求。)順便提一下,儘管名稱是歐洲的,但在尤拉發現拉丁方陣之前,就已經有人研究過它們,包括韓國數學家崔錫鼎,他比尤拉早出生約70年。

一個4階拉丁方陣。每個符號在每行每列中恰好出現一次。來源:Alejandro Vera Temiño Wikimedia (CC BY-SA 3.0)
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保關於塑造我們當今世界的發現和想法的有影響力的故事的未來。
作為一點澄清,雖然尤拉的論文被稱為“關於一種新型幻方的研究”,但今天大多數數學愛好者不會稱它們為幻方。一個n×n階的幻方使用1到n2之間的每個數字恰好一次,而拉丁方陣僅使用1到n之間的數字,但每個數字使用n次。
格雷科-拉丁方陣是一個n×n陣列中兩組n個符號的排列,使得每組符號形成一個拉丁方陣,並且沒有一對符號出現兩次。這個名稱可以使其更容易想象:第一組符號可以是拉丁字母表的前n個字母,第二組可以是希臘字母表的前n個字母。每個可能的拉丁字母和一個希臘字母的組合必須在格雷科-拉丁方陣中恰好出現一次。數字n是格雷科-拉丁方陣的階數。
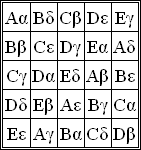
一個使用希臘字母和拉丁字母前五個字母的5×5格雷科-拉丁方陣。拉丁字母形成一個拉丁方陣,希臘字母也是如此,並且每個拉丁字母和一個希臘字母的組合都恰好出現一次。來源:Maksim Wikimedia
尤拉的研究使他得出結論,格雷科-拉丁方陣存在於奇數階和4的倍數階。不存在2階格雷科-拉丁方陣(您可以自己檢查),尤拉試圖構造一個6階的,但沒有成功,這使他推測不存在4n+2階的格雷科-拉丁方陣。關於不存在6階這種方陣的嚴格證明花了一些時間。(丹麥數學家托馬斯·克勞森聲稱他在1842年的一封信中證明了這一點,但該證明已遺失。 加斯頓·塔裡在1901年給出的證明是最早仍然存在的。)
研究人員開發了基於較小階方陣構造某些階格雷科-拉丁方陣的方法。例如,一個4階格雷科-拉丁方陣和一個3階格雷科-拉丁方陣可以組合形成一個12階格雷科-拉丁方陣。但他們的技術不適用於恰好有一個因子為2的階數,如2、6和10,因此他們沒有解決形式為4n+2的較大數字的問題。
最後,在1959年,Shrikhande、Raj Chandra Bose和Ernest Tilden Parker破解了這個密碼,發表了幾篇論文,完全解決了這個猜想,不僅證明了10、14、18等階的格雷科-拉丁方陣存在,而且還構造了某些維度的格雷科-拉丁方陣。他們贏得了“尤拉的破壞者”的綽號。(為了使其有效,你需要知道尤拉的發音像“oiler”,而不是“yooler”。)這篇文章頂部的圖片是一個彩色的10階格雷科-拉丁方陣的例子。
格雷科-拉丁方陣主要只是有趣,但它們在設計科學實驗中也有一些令人驚訝的實際應用。多米尼克·克萊夫和李·斯坦科斯基撰寫的一篇關於格雷科-拉丁方陣的論文指出,格雷科-拉丁方陣(以及更高階的類似方陣,在陣列中每個方框中不僅有兩個,而且有三個或更多符號)可用於設定實驗,在這些實驗中,許多不同的測試物件需要比較他們在幾個不同測試中的表現。檢視克萊夫和斯坦科斯基的文章,瞭解更多關於從尤拉到猜想“破壞”後幾十年問題歷史的資訊。要了解更多關於Shrikhande本人的資訊,請閱讀Nithyanand Rao的這篇文章,該文章是在Shrikhande 100歲生日之際撰寫的。
