本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
猴子!數學群!四維幾何!終於在一起了!
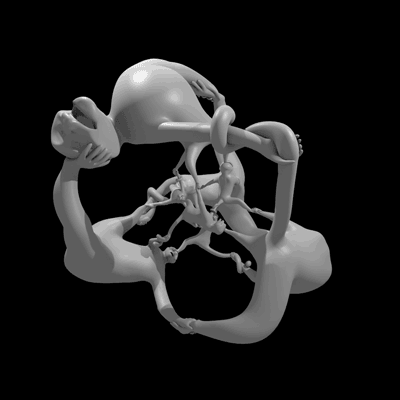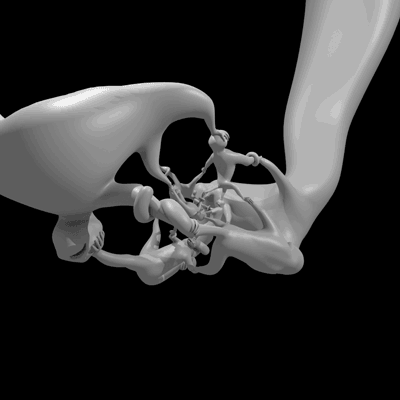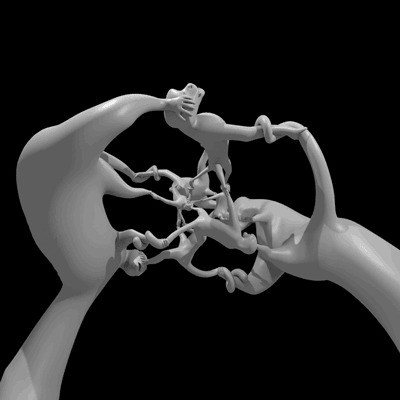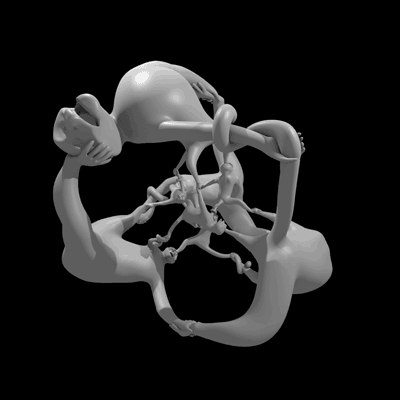
雕塑“猴子超立方體比什麼都好玩”在四維空間中旋轉的動畫。(由於我們感知的限制,我們實際上是在觀看四維物體的投影。)圖片來源:亨利·塞格曼和威爾·塞格曼。
這個名為猴子超立方體比什麼都好玩的雕塑,回答了一個懸而未決的問題:四元數群是否曾經作為某個物體的對稱群出現過?感謝數學家亨利·塞格曼和數學音樂家維·哈特,現在的答案是肯定的。他們關於這個雕塑的非常易懂的論文將發表在2014年Bridges數學-藝術會議的會議記錄中,您現在可以在預印本伺服器arxiv上免費閱讀。
關於支援科學新聞業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保關於塑造我們當今世界的發現和想法的有影響力的故事的未來。
為了理解猴子的含義,我們需要談談群。數學中“群”的含義比英語中的含義更具體。最抽象地說,群是一組元素和一個運算,該運算接受集合中的兩個元素並吐出第三個元素,並有一些額外的要求。例如,當您將兩個整數相加時,您會得到一個整數。群還需要有一個單位元素,一個保持其他元素不變的元素。對於整數,0 扮演著這個角色。群需要有逆元素:每個元素都必須有一個逆元素,以便當您將它們配對時,您會得到單位元素。對於整數,我們有相反數:+1 和 -1,+2 和 -2,等等。最後,群需要具有結合律:如果您將三個整數相加,例如 1+2+3,那麼您是先做 1+2(得到 3+3)還是先做 2+3(得到 1+5)都無關緊要。無論哪種方式,您最終都會得到 6。所有群都必須遵守該規則。但這些是唯一的規則,任何滿足這些規則的元素集合和運算都是一個群。
群不必像整數那樣是無限的。有限群的一個例子是數字1和-1與乘法運算。它只用兩個元素就滿足了所有規則。我們甚至可以從視覺上思考這個群,從變換的角度來看。元素1保持一切不變(它是單位元素),而-1則將事物沿一條線反射。如果您有一個具有雙邊對稱性的物體,您可以將其沿對稱線反射,物體看起來仍然相同。因此,-1變換代表了物體的對稱性。

這張蘋果的圖片(大部分)在沿藍線反射時保持不變。圖片來源:伊芙琳·蘭姆,基於 Rasback,透過維基共享資源 的照片。
如果雙邊對稱性是圖片或物體唯一的對稱性,那麼由1和-1以及乘法組成的群被稱為其對稱群。但是對於這張蘋果的圖片,我們也有旋轉對稱性。如果我們旋轉 1/5 圈,圖片仍然相同。讓我們將該旋轉命名為a。

這個蘋果的對稱性包括沿藍線的反射和標記為“a”的旋轉。圖片來源:伊芙琳·蘭姆,基於 Rasback,透過維基共享資源 的照片。
我們可以對圖片執行旋轉a最多 5 次,此時我們回到單位元素。我們還可以將這些旋轉中的任何一個與-1反射結合起來。最後,這張蘋果圖片的對稱群可以用元素1, -1, a, -a, a2, -a2, a3, -a3, a4, 和 -a4來表示。(您可以在維基百科的 二面體群 頁面上閱讀更多關於為什麼這些是此對稱群的唯一元素的資訊。)
群和對稱性之間的關係一直是研究具有對稱性的物體和群本身的一種有用的方法。在他們的論文中,哈特和塞格曼提出了一些關於群和對稱性的問題
“1. 哪些群可以表示為某些真實世界物理物體的對稱群?
2. 哪些群實際上已被表示為某些真實世界物理物體的對稱群?
3. 是否存在任何明顯的差距——小的、美麗的群,它們應該在對稱物體中具有物理表示,但到目前為止還沒有?”
他們專注於問題#3:確實存在一個小的、美麗的群,即四元數群,到目前為止它還沒有物理表示。它只有 8 個元素:1, -1, i, -i, j, -j, k, 和 -k。這是它的乘法表。(在這個群中,乘法順序很重要,左邊的元素在頂部的元素之前。所以 ij=k,但 ji=-k。)
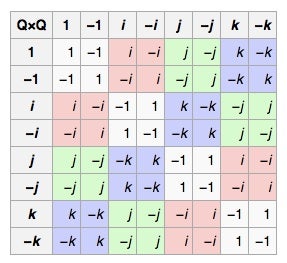
四元數群的乘法表。
數字 1 和 -1 的行為正常。數字 i、j 和 k 的平方都為 -1(所以它們有點像 虛數),並且 i、j 和 k 之間存在迴圈關係:ij=k,jk=i,ki=j。(如果您學過物理或多元微積分,這可能會讓您想起叉積。)
四元數群尚未作為物理物體或藝術品的對稱群出現的一個原因是,它不是平面或三維空間對稱群的子群。換句話說,在二維或三維空間中,不存在任何旋轉、平移和反射的組合,可以保持空間完整並具有四元數群的結構。
但是,由於哈特和塞格曼是富有創造力、意志堅定的人,他們並沒有被像三維幾何約束這樣的小細節嚇倒!四元數群是四維空間對稱群的子群,所以他們做了合乎邏輯的事情,將維度提升了一維。塞格曼已經視覺化四維物體投影一段時間了。(我在 2012 年寫過關於它的文章。)如果您有一個三維物體,您可以將其二維視覺化的方法之一是將光源對準它,並檢視其在牆上的陰影。塞格曼和他的合作者使用了類似的技術,維度提升了一維,製作了四維物體投影的 3D 列印件。塞格曼在 YouTube 上發表了一個關於該技術的一小時演講,他和索爾·施萊默在 這裡 (pdf) 寫了關於該技術的文章。
這個雕塑,除了上面的動畫之外,還藉助 3D 列印的魔力實現了物理實體,由塞格曼和他的兄弟威爾設計。他們從四維立方體的類比物開始,有時稱為 超立方體、四方體或 8-胞體。超立方體的對稱群比四元數群更大,所以他們必須做一些事情來減少對稱性的數量。這就是猴子出現的地方。為了減少對稱性的總數,他們在超立方體的 8 個立方體中的每一個的中心放置了一隻猴子。* 每隻猴子都有兩條胳膊、兩條腿、一條尾巴和一個頭。這使得只有少數幾種方法可以扭轉和轉動物體,並且仍然保持猿類附肢的位置。透過正確的猴子方向,他們設法將對稱性限制到足以獲得四元數群。(有關完整詳細資訊,我敦促您閱讀 該論文。)然後,就是使用塞格曼的投影技術使猴子成為現實的問題。就像在牆上製作皮影戲一樣,投影會扭曲尺寸。因此,猴子在四維空間中尺寸相同,但它們在三維空間中的投影使其中一些看起來更大。
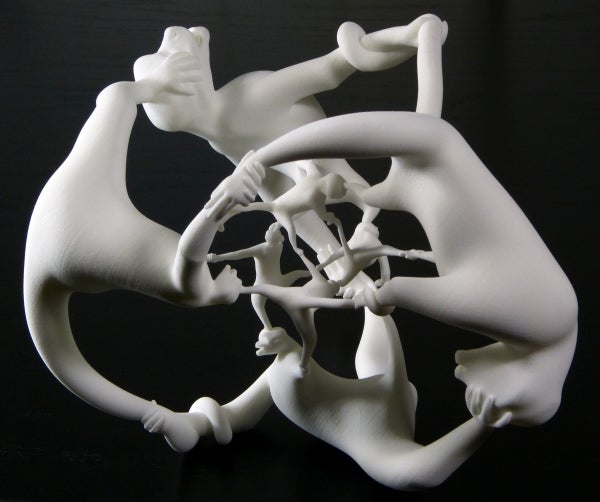
猴子超立方體比什麼都好玩,一個具有四元數群對稱性的雕塑。圖片來源:亨利·塞格曼和威爾·塞格曼。
我希望哈特、塞格曼和塞格曼(以及其他數學藝術家)將繼續將其他被忽視的群變成對稱群。我希望能看到一個怪獸的怪獸群!
*更正:這句話最初宣告在超立方體的每個頂點都有一隻猴子。在超立方體的每個立方體中都有一隻猴子。