本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
在今天的播客“我最喜歡的定理”節目中,我的聯合主持人凱文·克努森和我很高興與悉尼大學的應用數學家納莉妮·喬希交談。(我們特別高興能成為這一集的時間旅行者。凱文和我在星期四下午錄製,而喬希博士在星期五早上加入了我們。)您可以在這裡或 kpknudson.com 收聽這一集,那裡也有文字稿。
喬希博士選擇與我們分享複分析中的米塔-列夫勒定理。如果您沒有複分析的背景,這裡的一些背景知識可能會幫助您理解本集中的主要思想。
關於支援科學新聞業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞業 訂閱。透過購買訂閱,您正在幫助確保關於塑造我們今天世界的發現和想法的具有影響力的故事的未來。
複分析處理複平面上的函式。複平面上的點具有 x+iy 的形式,其中 x 和 y 是實數,i 是 -1 的平方根。但複平面的真正威力在於,透過將自然具有兩個座標的平面上的點視為單個數字,微積分變得更加強大。
我們也可以在複平面上定義所有正常的微積分內容。例如,導數,即函式在某一點的變化率,在複平面上是有意義的。但是,對於一個函式來說,在複平面上的某一點完全可微或解析,比函式在多元微積分意義上具有導數要困難得多。這忽略了很多內容,但主要的結論是,您可以將解析函式視為光滑的。
與處處解析的函式(也稱為全純函式)密切相關的是亞純函式。這些函式在除稱為極點的孤立點之外的所有地方都是解析的,在極點處,函式以某種受控的方式爆發。喬希博士用火山點綴景觀的生動形象來描述亞純函式。除了火山之外,景觀是平滑而溫和的。
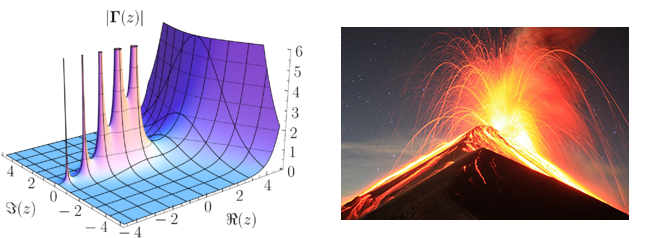
左圖:亞純函式的圖。右圖:瓜地馬拉的富埃戈火山爆發。這兩張圖片幾乎無法區分。圖片來源:Geek3 維基共享資源(CC BY-SA 3.0)(左), Kevin.Sebold 維基共享資源(CC BY-SA 3.0)(右)
米塔-列夫勒定理,以瑞典數學家戈斯塔·米塔-列夫勒(Gösta Mittag-Leffler,1846-1927)的名字命名,涉及複雜的“法醫分析”,這個術語是我剛剛編造的。它說,如果您知道極點的位置以及函式在極點周圍的行為或用喬希博士的話說“強度”,您基本上可以重建一個亞純函式。這些資訊足以重建函式,至少在一定程度的擺動空間內。
我很驚訝一位應用數學家選擇了一個似乎是純粹的複分析定理,我認為複分析不是非常應用(儘管這可能僅僅是因為我個人與它的關係)。但喬希博士告訴我們米塔-列夫勒定理的宏大思想,即獲取區域性資訊並將其轉化為全域性資訊的思想,對她構建數學“工具箱”以幫助人們解決現實世界問題的工作非常重要。(如果您像我一樣對她隨意提及墨西哥庫埃納瓦卡公共汽車的數學感到好奇,請檢視皮奧特·瓦爾喬夫的這篇 arxiv 論文。)
在播客的每一集中,我們都會要求我們的嘉賓將他們的定理與生活中的食物、飲料、藝術、音樂或其他樂趣搭配。喬希博士出生於緬甸,並選擇了 htamin le thoke,一種混合了多種食材的緬甸米飯沙拉。像早期的嘉賓艾米·拉頓斯卡婭一樣,她也建議史蒂夫·萊奇作為合適的音樂伴奏。您必須收聽這一集才能瞭解le thoke 和萊奇為什麼與米塔-列夫勒定理完美搭配。
您可以在她的網站、Twitter 或她的著作 離散系統與可積性 中找到喬希博士。有關米塔-列夫勒定理及其歷史的更多資訊,請檢視勞拉·E·特納在Historia Mathematica 上發表的 這篇文章。您可以在 kpknudson.com 和 Unity 之根 找到有關本播客中數學家和定理的更多資訊,以及其他令人愉悅的數學佳餚。 文字稿可在此處獲取。 您可以 在 iTunes 和其他播客交付系統上訂閱和評論播客。 我們很樂意聽到聽眾的來信,請傳送郵件至 myfavoritetheorem@gmail.com。凱文·克努森在 Twitter 上的賬號是 @niveknosdunk,我的賬號是 @evelynjlamb。該節目本身也有一個 Twitter 賬號:@myfavethm 和一個 Facebook 頁面。請在下次加入我們,瞭解另一個引人入勝的數學知識。
“我最喜歡的定理”節目回顧
第 0 集:主持人最喜歡的定理 第 1 集:艾米·威爾金森最喜歡的定理 第 2 集:戴夫·裡切森最喜歡的定理 第 3 集:艾米莉·戴維·勞倫斯最喜歡的定理 第 4 集:喬丹·艾倫伯格最喜歡的定理 第 5 集:杜莎·麥克達夫最喜歡的定理 第 6 集:海倫中榮最喜歡的定理 第 7 集:亨利·福勒最喜歡的定理 第 8 集:賈斯汀·柯里最喜歡的定理 第 9 集:艾米·拉頓斯卡婭最喜歡的定理 第 10 集:穆罕默德·奧馬爾最喜歡的定理 第 11 集:珍妮·克萊蘭最喜歡的定理 第 12 集:坎迪斯·普萊斯最喜歡的定理 第 13 集:帕特里克·霍納最喜歡的定理 第 14 集:勞拉·塔爾曼最喜歡的定理 第 15 集:費德里科·阿迪拉最喜歡的定理 第 16 集:賈亞德夫·阿特雷亞最喜歡的定理
