本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
上個月,我寫了一篇關於我每天早上在 Facebook 上玩的一個小數學遊戲。我檢視哪些朋友那天過生日,哪些朋友互相認識,哪些朋友互不相識。通常情況是兩者兼有,但當只有其中一種情況時,我會感到興奮。
與這種情況相關的數學分支稱為拉姆齊理論。它處理許多不同的情況,在這些情況下,我們想要計數事物,並檢視某些配置(即所有朋友或所有陌生人)是否必然出現。在上個月的文章中,我提到了拉姆齊數,它與派對上的共同朋友或陌生人有關。具體來說,拉姆齊數 R(m,n) 是你必須邀請參加派對的最小人數,以保證m 個人都互相認識,或者 n 個人都是陌生人。例如,如果你邀請六個人參加派對,你保證會得到一個由三個互相認識的朋友組成的小團體,或者一個由三個互相不認識的陌生人組成的群體,他們尷尬地盯著彼此在潘趣酒碗旁。所以 R(3,3)=6。
(朋友或陌生人的背景並非真正必要。我們可以將每個人想象成圖中的一個點,如果兩個人互相認識,則用藍線連線,如果他們互不相識,則用紅線連線。)
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和思想的具有影響力的故事的未來。
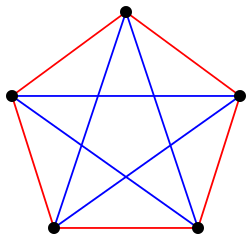
一個有五個人參加的派對中的社交關係圖。兩個人如果是朋友,則用藍線連線,如果是陌生人,則用紅線連線。這張圖片證明 R(3,3) 必須大於 5,因為每個三角形都有兩條藍色邊和一條紅色邊,或者兩條紅色邊和一條藍色邊。
圖片來源:Richtom80 Wikimedia (CC BY-SA 3.0)
我們對拉姆齊數的知識限制令人驚訝。我們知道 R(3,3)=6,但如果我們正在尋找一種方法來保證只有四個共同的朋友或陌生人,我們必須邀請 18 個人,這是一個相當大的跳躍。我們甚至不知道五個共同朋友或陌生人的答案。它介於 43 和 49 之間[更新:在 2017 年 3 月,Vigleik Angeltveit 和 Brendan D. McKay將 R(5,5) 的上限從 49 降低到 48],但我們尚未準確地確定它。
當我在研究我關於拉姆齊理論和 Facebook 的文章時,我看到了 這段引言,它來自 多產的數學家保羅·埃爾德什,出自羅納德·格雷厄姆和喬爾·斯賓塞 1990 年在《大眾科學》上發表的文章。
假設外星人入侵地球,並威脅說如果人類在一年內找不到紅色五和藍色五的拉姆齊數,就會將地球摧毀。我們可以召集世界上最聰明的人才和最快的計算機,並且在一年內我們可能會計算出這個值。然而,如果外星人要求紅色六和藍色六的拉姆齊數,我們將別無選擇,只能發動先發制人的攻擊。
換句話說,如果外星人正在尋找 R(5,5),我們會嘗試計算出 R(5,5)。如果他們正在尋找 R(6,6),我們會嘗試找出如何擊敗外星人。誠然,這是一個愚蠢的假設,但是什麼時候阻止過任何人?
僅僅為了好玩,我決定進行一些粗略的計算,看看摩爾定律對計算機處理能力的影響可能對那句話產生什麼影響。如果埃爾德什今天說這句話,他是否需要更改數字?將摩爾定律解釋為自 1990 年以來計算速度每 18 個月翻一番,計算速度應該提高了約 217 倍,或 131,072 倍。這非常令人鼓舞。如果我們在 1990 年可以用一年時間計算出 R(5,5),那麼今天只需要幾分鐘。(記住,這是假設我們使用了世界上所有最聰明的人才和最快的計算機。)
那麼 R(6,6) 呢?它比 R(5,5) 困難多少?我們知道 R(5,5) 介於 43 和 49 之間。例如,一組 45 個人可能以許多不同的方式相互聯絡。45 個人之間共有 990 種成對關係,每種關係可能是友誼或陌生。那是 2990,大約是 10298,不同的朋友和陌生人配置,我們必須篩選這些配置,在每一種配置中尋找 5 個共同朋友或共同陌生人的集合。(作為參考,宇宙中大約有 1080 個原子。)
對於六個朋友或陌生人,我們遇到了更大的麻煩。我們知道 R(6,6) 介於 102 和 165 之間。在低端,有大約 101550 種可能性需要檢查 102 個人。這比我們在 R(5,5) 中看到的可能性大約多 101250 倍,遠遠超過了我們從摩爾定律獲得的 131,072 倍的加速因子。
現在,圖的絕對數量並不是一切。有一些方法可以減少您必須檢查的可能性數量。由於我不是拉姆齊理論家,我不知道所有這些方法,所以我不知道這個問題可以簡化多少。我確信可能性的數量可以減少許多數量級, 但我願意打賭,即使我們將計算速度提高 131,072 倍,101250 這個數字也代表著一個障礙,使得 R(6,6) 比 R(5,5) 難以逾越。
所以我的結論是,與找到 R(6,6) 的計算成本相比,摩爾定律只是滄海一粟。祝賀你,殭屍埃爾德什,你贏了這一輪!如果我們真的受到強大但又異常一心一意的外星人攻擊, 他們的目的是摧毀地球,除非我們告訴他們 R(6,6),否則我們仍然必須與他們戰鬥。