本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
在這一集“我最喜歡的定理”中,我的聯合主持人凱文·努森和我很高興與哈維·穆德學院的數學教授 Mohamed Omar 交談。您可以在這裡收聽這一集,或者在 kpknudson.com 收聽。
奧馬爾博士最喜歡的定理是伯恩賽德引理。數學家通常使用“引理”這個詞來表示一個較小的定理,或者是在證明一個更大的定理時使用的定理,但這個引理本身就是一個令人印象深刻的定理。(正如奧馬爾博士指出的那樣,這個定理甚至不是來自一位名叫伯恩賽德的數學家。因此,如果伯恩賽德部分不正確,那麼引理部分也可能不正確,我們可以將其提升為定理的地位。)
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續講述關於塑造我們今天世界的發現和想法的具有影響力的故事。
伯恩賽德引理 涉及組合數學和代數。組合數學基本上是計數。雖然這比用手指計數要難一點。您可能試圖確定一副牌中可能有多少個滿堂紅,或者在棋盤上可以有多少種排列棋子的方式。代數通常是對數學物件集合中的對稱性和關係的研究。因此,伯恩賽德引理解決了物件的對稱性如何影響其組合數學。
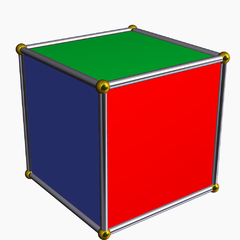
一個面被塗成紅色、綠色和藍色的立方體。伯恩賽德引理可以幫助您計算有多少種基本不同的方法來給面著色。圖片來源:Stella Software,作者:Robert Webb Wikimedia
所有這些都有點抽象,但奧馬爾博士給了我們一個非常具體的例子來思考。你從一個立方體開始,你可以給每個面塗上紅色、綠色或藍色。你可以用多少種不同的方法來給它著色?僅使用這些資訊,每個面都有 3 種顏色選擇,共有 6 個面,因此您得到 36 或 729 種可能的著色方式。但是,如果以這種方式計數,事情就會變得有點愚蠢。頂部面為紅色而所有其他面為綠色的立方體與底部面為紅色而所有其他面為綠色的立方體不同。但是,只需將其翻轉過來,就可以輕鬆地將其中一個立方體變成另一個立方體。您可能希望將這兩種著色方式視為相同,以及任何兩種著色方式,對於這兩種著色方式,您可以拿起其中一種並旋轉它以獲得另一種。
這就是伯恩賽德引理的用武之地。它允許您使用立方體的對稱性集合(形成一個稱為群的結構)來更準確地計算可能的著色方式。並且該引理不僅適用於立方體和著色。任何時候您研究具有某些對稱性集合的物件的配置或構象(即使是非常抽象的對稱性),您都可以使用伯恩賽德引理來計數它們。我們在播客中使用了一些代數術語。如果您想了解有關其中一些術語的更多資訊,這裡有一些連結:群(或 如果您喜歡詩歌形式的定義,請點選此處);軌道和穩定器;軌道-穩定器定理(適用於具有較強數學背景的人)。
在播客的每一集中,我們都會請嘉賓將他們的定理與某物配對:食物、飲料、音樂、文學或生活中的任何其他樂趣。奧馬爾博士選擇將伯恩賽德引理與棋盤大理石蛋糕搭配。您必須收聽這一集才能找出為什麼這與伯恩賽德引理完美搭配。
您可以在奧馬爾博士的 網站、Twitter 或他的著作 《走向 RSA 密碼學的數論》 中找到他。您可以在 kpknudson.com 和 Unity 之根 找到有關此播客中數學家和定理的更多資訊,以及其他令人愉悅的數學知識。 此處提供文字稿。您可以在 iTunes 和其他播客分發系統上 訂閱和評論播客。我們很樂意聽到聽眾的來信,請傳送郵件至 myfavoritetheorem@gmail.com 聯絡我們。凱文·努森在 Twitter 上的賬號是 @niveknosdunk,我的賬號是 @evelynjlamb。該節目本身也有一個 Twitter 賬號:@myfavethm 和一個 Facebook 頁面。下次加入我們,學習另一個引人入勝的數學知識。
之前在“我最喜歡的定理”節目中
第 0 集:主持人最喜歡的定理 第 1 集:Amie Wilkinson 最喜歡的定理 第 2 集:Dave Richeson 最喜歡的定理 第 3 集:Emille Davie Lawrence 最喜歡的定理 第 4 集:Jordan Ellenberg 最喜歡的定理 第 5 集:Dusa McDuff 最喜歡的定理 第 6 集:Eriko Hironaka 最喜歡的定理 第 7 集:Henry Fowler 最喜歡的定理 第 8 集:Justin Curry 最喜歡的定理 第 9 集:Ami Radunskaya 最喜歡的定理
