本文發表於《大眾科學》的前部落格網路,僅反映作者的觀點,不一定反映《大眾科學》的觀點。
與 π 和 e 一樣,黃金比例 也是一個數字名人。它是一個非常特殊的矩形邊長的比率。如果你取這個矩形,並從中切下儘可能大的正方形,你剩下的另一個矩形與第一個矩形具有完全相同的邊長比率。這種構造定義了邊長之間獨特的關系,任何邊長具有這種關係的矩形都稱為黃金矩形。如果黃金矩形的短邊長為 1,則長邊長為 (1+√5)/2,約為 1.618。
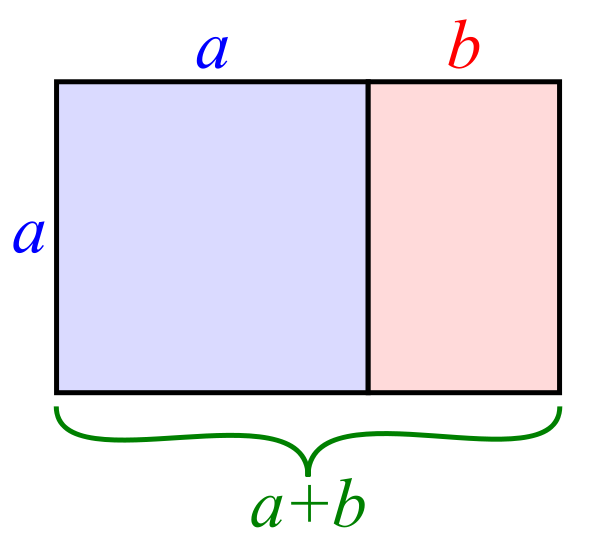
一個“黃金矩形”可以被切割成一個正方形和另一個黃金矩形。a+b 與 a 的比率與 a 與 b 的比率相同。
黃金比例對於許多數學愛好者來說都很熟悉,但你聽說過白銀比例嗎?青銅比例呢?這些是其他類似構造的無理數,它們不如其華麗的黃金錶親那樣廣為人知。與黃金比例一樣,每個所謂的金屬平均數都可以被視覺化為特殊矩形上的邊長比率。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保關於塑造我們當今世界的發現和想法的具有影響力的故事的未來。
對於白銀比例,我們希望切掉兩個正方形,並剩下一個與第一個矩形具有相同縱橫比的矩形。
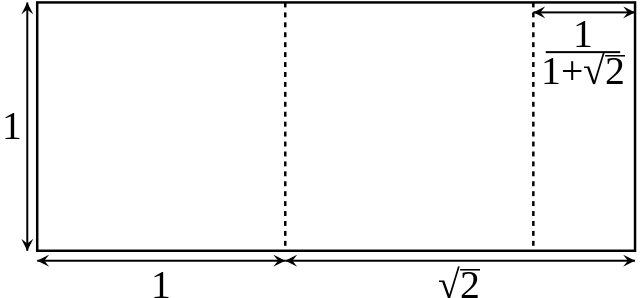
一個“白銀矩形”可以被切割成兩個正方形和另一個白銀矩形。邊長比率為 1+√2,約為 2.414。圖片來源:Krishnavedala,來自維基共享資源。
對於青銅比例,我們希望切掉三個正方形,最終得到一個相似的矩形。
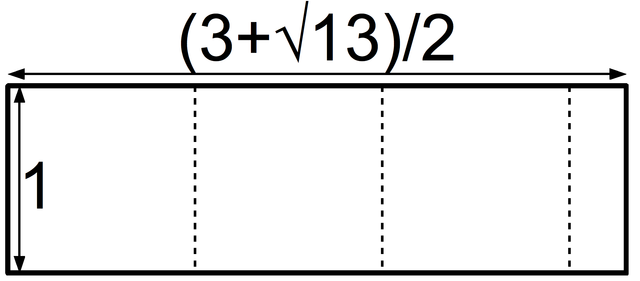
一個“青銅矩形”可以被切割成三個正方形和另一個青銅矩形。青銅比例為 (3+√13)/2,約為 3.303。圖片來源:Hyacinth,來自維基共享資源。
除了黃金、白銀和青銅之外,對於金屬的珍貴程度或期望值並沒有規範的排序,但我們可以繼續建立這些比例。我們可以將下一個稱為紫銅比例。“紫銅矩形”可以被切割成四個正方形和另一個紫銅矩形,紫銅比例將為 2+√5,或約 4.24。
隨著我們不斷前進,也許下一個是鎳或鋁,矩形會變得越來越長,因此不難看出,每個金屬平均數都比上一個大,就像黃金比例介於 1 和 2 之間一樣,白銀比例介於 2 和 3 之間,青銅比例介於 3 和 4 之間,並且模式繼續:第 n 個金屬平均數始終介於整數 n 和 n+1 之間。
黃金比例與 著名的斐波那契數列 1、1、2、3、5…… 有著有趣的關係,其中每一項都是前兩項之和。隨著斐波那契數列的項數增加,相鄰項之間的比率接近黃金比例。同樣,其他金屬平均數也與其他數列有這些關係。對於白銀比例,它是佩爾數列。它從 0、1、2、5、12、29…… 開始。第 n 項是第 (n-2) 項和 2 倍的第 (n-1) 項之和。對於青銅平均數,公式中有 3 而不是 2,依此類推。
當我與威斯康星大學麥迪遜分校的應用數學家 Jean-Luc Thiffeault 談論太妃糖拉伸機時,我瞭解了金屬平均數。在他最近的一篇 論文 中,他對歷史悠久的太妃糖拉伸機專利進行了數學分析,根據它們在每次透過拉伸機時拉伸糖果的程度對其進行分類。因此,如果你每次拉伸都將太妃糖的長度加倍,那麼你的拉伸比率將為 2。他發現一些太妃糖拉伸機的拉伸比率基於黃金比例和白銀比例。
你實際上可以在 1918 年的黃金比例太妃糖拉伸機專利中看到黃金比例與斐波那契數列之間的關係。齒輪的運動意味著手柄的每次轉動基本上都會將前兩個步驟加在一起。如果我們的原始太妃糖塊(下圖左上角)的長度為 1,則下一步的長度為 2。然後下一步的長度為 3,下一步為 5,依此類推。隨著時間的推移,拉伸比率將趨向於黃金比例,我們可以看到斐波那契數列的步驟如何將我們帶到那裡。
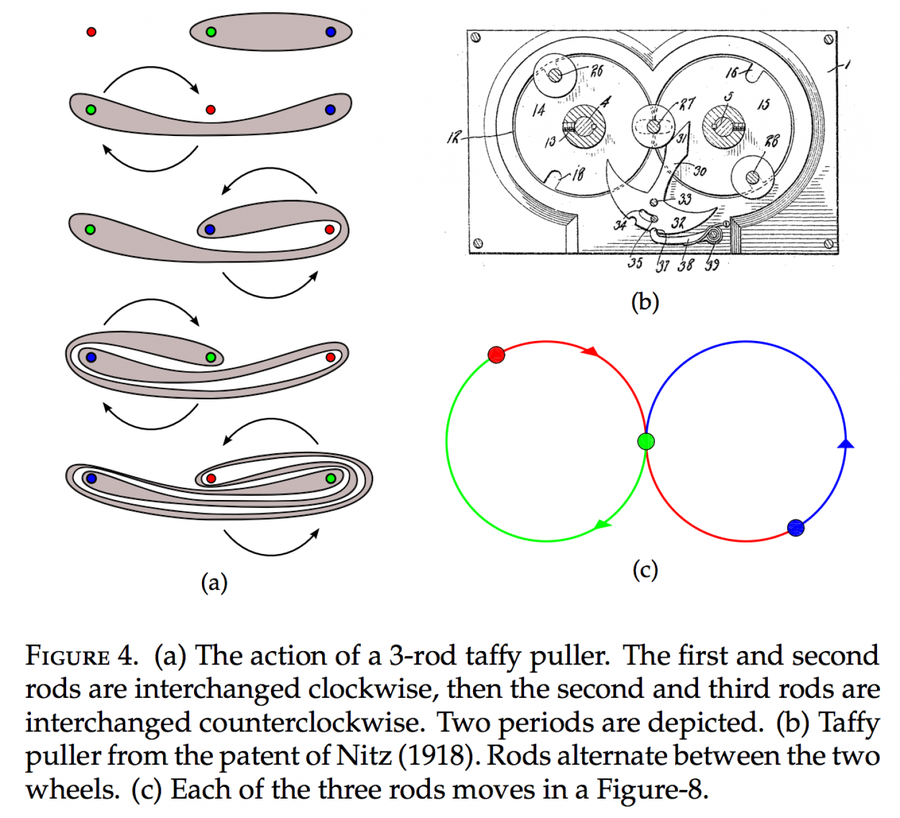
在 我在史密森尼網站上發表的文章 中閱讀更多關於太妃糖拉伸的數學原理。
