本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
有一個老套的關於數學家的笑話(或者工程師,甚至是芬蘭人),說如果你和一個數學家交談時,他們看著你的鞋子,你就能知道他們是外向型的。事實上,數學家有各種形狀、大小、顏色和外向程度,但是向下看可能會在數學上有所收穫。在一次去德國拜訪一些數學家朋友的旅行中,我盯著地面看,結果絆倒了——幾乎真的被一塊美麗的瓷磚圖案絆倒了。以下是我盯著它看時的一些粗略的想法記錄。
多麼漂亮的瓷磚!我想我以前從未見過這樣的瓷磚。或者即使見過,我也沒注意到。 這些形狀有多少條邊?1、2、3、4,然後它們都是成對的。八條。這是一個八邊形瓷磚。

用白色輪廓勾勒出一個八邊形的瓷磚。圖片來源:伊芙琳·蘭姆
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您將幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和思想的具有影響力的故事。
非凸形狀看起來與凸形狀如此不同,這難道不有趣嗎?你不能用正八邊形平鋪歐幾里得平面。我想即使這些形狀各有八條邊,但它們實際上只是偽裝成平行四邊形或矩形。這種瓷磚的底層圖案只是一個網格。

我在一些八邊形的中心點上打點,然後用綠色連線它們,以突出顯示瓷磚的底層平行四邊形網格。 圖片來源:伊芙琳·蘭姆
這些八邊形有四對平行邊。這意味著它們是平移曲面! 我敢打賭我的配偶會喜歡這個。他真的很喜歡平移曲面。
在這裡,我打斷我的意識流回憶,來定義一下平移曲面。它是一個或多個多邊形的集合,其中邊成對出現,並且平行且長度相同。你可以想象將這些邊對粘合在一起,將平面多邊形變成一個在空間中彎曲的曲面。環面,或甜甜圈,是一個你可以在家輕鬆製作的例子。

一個標有邊配對的八邊形。具有相同標籤的邊長度相同且平行。圖片來源:伊芙琳·蘭姆
如果你在一個平移曲面上將相對的邊粘合在一起,你會得到某種甜甜圈,也許是帶有多孔的甜甜圈。我想知道用這個會得到什麼樣的甜甜圈。嘿,這附近有甜甜圈店嗎?沒有?我寧願要一個椒鹽捲餅。
我很難想象如果我將對應的邊粘合在一起會發生什麼。等等,雙正五邊形不是有八條邊嗎?
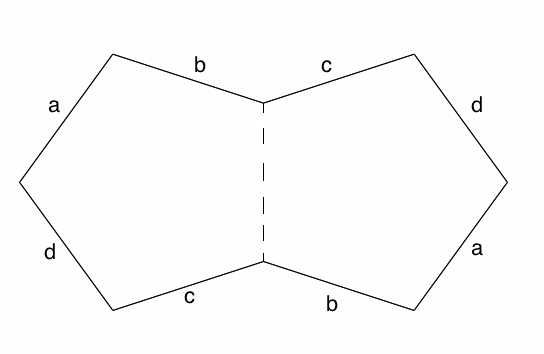
雙正五邊形的圖示,兩個五邊形沿虛線粘合在一起。標有相同字母的邊可以粘合在一起以建立一個曲面。圖片來源:伊芙琳·蘭姆
戴安娜·戴維斯關於雙五邊形的“用舞蹈演繹你的博士論文”影片太酷了!我應該再看一遍!
雙五邊形上的切割序列,透過舞蹈解釋,來自 戴安娜·戴維斯,在 Vimeo 上。
鋪路石中的八邊形與雙五邊形具有相同的平行邊模式,因此它們必定粘合成與雙五邊形相同型別的曲面。這是一個虧格為 2 的曲面,或是一個有兩個孔的甜甜圈。說真的,我現在真的很想吃一些糕點。
等等,如果雙五邊形是一個八邊形,那一定有辦法像雙五邊形那樣將鋪路石八邊形切割成五邊形對!
.jpg?w=350)
一張將其中一個八邊形切割成兩個五邊形的圖片。圖片來源:伊芙琳·蘭姆
這意味著這個八邊形瓷磚也是偽裝成五邊形瓷磚!我喜歡五邊形瓷磚!我是否發現了一種用五邊形平鋪平面的新方法?!!

五邊形瓷磚用白色勾勒出來。圖片來源:伊芙琳·蘭姆
這不太可能,對吧?我敢打賭,任何帶有直角的五邊形瓷磚很久以前就被發現了。我回家後必須查一下。
的確,當我稍後查閱時,我發現這個五邊形與下圖中的第一種型別的五邊形瓷磚相同。這已經為人所知一段時間了。

我該如何平鋪你呢?讓我數數方法... 圖片來源:Ed Pegg Jr. Wikimedia(CC BY-SA 4.0)
五邊形中的角是多少度?我沒有量角器,但我猜大概是 90-90-130-60-170。
您可能會注意到,鋪路石八邊形的角度與圖表左上角的八邊形角度不完全相同。好眼力!已知有 15 種類型的五邊形可以平鋪歐幾里得平面,但其中一些型別具有一些自由度,整個五邊形族都可以平鋪平面,因為它們滿足相同的基本規則。第一種型別的五邊形瓷磚包括任何兩個相鄰角之和為 180° 的五邊形。
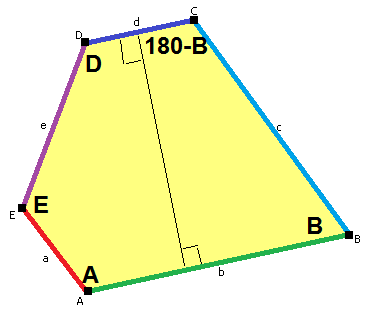
任何滿足上述溫和條件的五邊形,即具有兩個相鄰角之和為 180° 的五邊形,都可以平鋪平面。圖片來源:Tomruen Wikimedia(CC BY-SA 4.0)
盯著這個瓷磚幫助我理解了為什麼這種五邊形可以平鋪平面。有些點是三個非直角匯聚在一起,有些點是直角與形狀的一條邊匯聚在一起。任何具有這種性質的五邊形都必須可以平鋪平面!
所以這是一個八邊形瓷磚,它也是一個五邊形瓷磚,它建立在底層的四邊形瓷磚網格之上。這有多酷?德國有很多這樣的瓷磚嗎?我應該搬到德國去。
如果我沒有注意到這些不尋常的瓷磚並停下來欣賞一會兒,我就永遠不會花時間思考為什麼這種特定型別的五邊形可以平鋪平面,並自己弄清楚,而不是聽信別人的話。有時候,盯著你的腳下看並不是一件壞事。
要了解更多#foundmath,請在 Instagram 上關注我。
