本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
在“我最喜歡的定理”這一集中,我的共同主持人凱文·克努森和我很高興與詹姆斯·麥迪遜大學的數學教授勞拉·塔爾曼交談。您可以在這裡或kpknudson.com收聽這一集。
塔爾曼博士多年來戴過許多數學家的帽子,她研究的領域之一是紐結理論。紐結理論學家研究數學紐結,這幾乎與您的鞋帶或手機充電器線上的紐結相同。您只需將鞋帶或線的末端粘在一起,即可得到數學家研究的那種紐結。
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您將幫助確保關於塑造我們當今世界的發現和想法的有影響力的故事的未來。
紐結通常以二維圖的形式呈現,其中線束相互交叉,紐結理論中最基本的問題是,紐結的兩個圖何時實際上是同一個紐結。
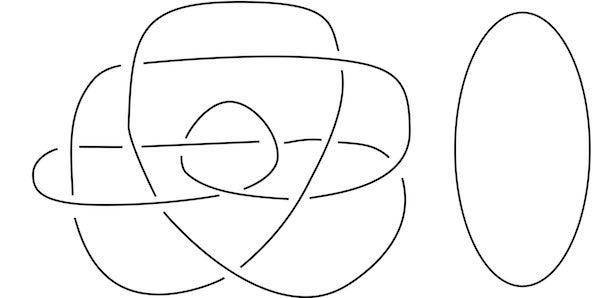
同一個紐結(解結)的兩個圖。左圖來自Mitsuyuki Ochiai的計算機紐結理論導論。來源:基於C S 和 Pbroks13 Wikimedia (CC BY-SA 3.0)
在20世紀20年代,庫爾特·萊德邁斯特和其他人表明,如果兩個紐結是相同的,則可以使用有限的萊德邁斯特移動序列將一個圖變成另一個圖。
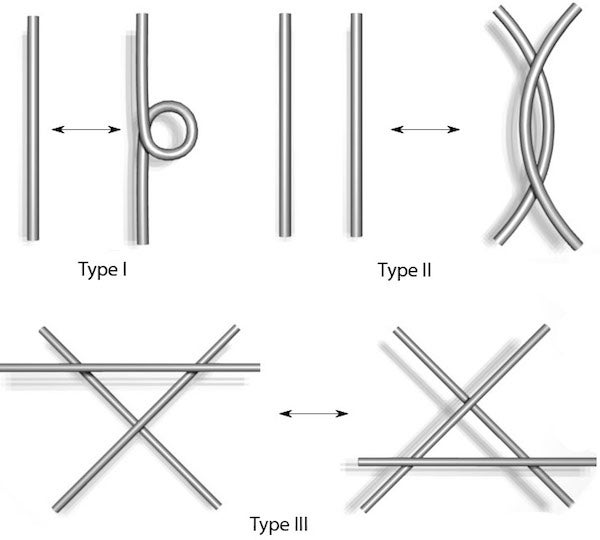
一個圖表,說明了三種類型的萊德邁斯特移動。來源:伊芙琳·蘭姆,基於Yamashita MakotoWikimedia (CC BY-SA 3.0) 的作品
但是,知道可以使用萊德邁斯特移動將兩個等效的紐結圖轉換為相同的圖,其效用是有限的。如果您有兩個圖並且無法將一個圖轉換為另一個圖,您如何判斷這是因為紐結實際上是不同的,而不是因為您只是沒有找到正確的移動序列?
塔爾曼最喜歡的定理提供了一種確定紐結是否等效於解結(一個簡單的圓圈)的方法。它表明,如果紐結實際上是解結,則根據紐結圖中交叉點的數量,將紐結簡化為圓圈所需的萊德邁斯特移動次數存在上限。如果您嘗試每個可能的移動序列,該序列至少與該上限一樣長,並且您的圖永遠不會變成圓圈,那麼您就可以確定該紐結確實是一個紐結,而不是一個解結。(快速說十遍。)
塔爾曼喜歡這個定理,不僅因為它第一次明確給出了這個問題的上限,而且還因為它給出的上限非常誇張。在證明該定理的原始論文中,喬爾·哈斯和傑弗裡·拉加里亞斯得到的上限為2n1011,其中n是圖中交叉點的數量。那是2的n 百億次方。哎呀!當您嘗試將該數字輸入線上計算器Wolfram Alpha時,即使對於非常少的交叉點,計算器也會宕機。
塔爾曼博士還向我們介紹了另一篇論文,這篇論文由亞歷山大·考沃德和馬克·拉肯比撰寫,該論文限制了顯示任意兩個給定紐結圖是否等效所需的萊德邁斯特移動次數。該界限涉及冪塔,冪塔的數值也以驚人的速度變得非常大。它們大到我無法描述它們有多大。

為紐結理論和巨大的數字舉杯!來源:Maman Voyage Flickr (CC BY-ND 2.0)
在每一集中,我們都會要求嘉賓將他們的定理與某些東西配對。塔爾曼博士選擇了一杯美味的香檳來慶祝她最喜歡的定理。您必須收聽這一集才能瞭解她為什麼認為這與紐結定理完美匹配。
除了教學和研究工作外,塔爾曼博士還曾在國家數學博物館擔任駐館數學家一個學期,並在3D列印行業工作過。她現在在課堂上使用3D列印,並在她的部落格Hacktastic上釋出3D列印教程。她的網站是mathgrrl.com,她的Twitter賬號是@mathgrrl。
您可以在kpknudson.com和統一之根找到有關此播客中數學家和定理的更多資訊,以及其他令人愉快的數學知識。此處提供文字記錄。您可以在iTunes和其他播客分發系統上訂閱和評論播客。我們很樂意聽到聽眾的來信,請傳送郵件至myfavoritetheorem@gmail.com。凱文·克努森在Twitter上的賬號是@niveknosdunk,我的賬號是@evelynjlamb。該節目本身也有一個Twitter feed:@myfavethm和一個Facebook頁面。請在下次加入我們,瞭解另一個引人入勝的數學知識。
以前在“我最喜歡的定理”節目中
第 0 集:您主持人的最喜歡的定理 第 1 集:艾米·威爾金森最喜歡的定理 第 2 集:戴夫·裡切森最喜歡的定理 第 3 集:埃米爾·戴維·勞倫斯最喜歡的定理 第 4 集:喬丹·埃倫伯格最喜歡的定理 第 5 集:杜薩·麥克達夫最喜歡的定理 第 6 集:惠理子·廣中 最喜歡的定理 第 7 集:亨利·福勒最喜歡的定理 第 8 集:賈斯汀·柯里最喜歡的定理 第 9 集:艾米·拉頓斯卡婭最喜歡的定理 第 10 集:穆罕默德·奧馬爾最喜歡的定理 第 11 集:珍妮·克萊蘭 最喜歡的定理 第 12 集:坎迪斯·普萊斯最喜歡的定理 第 13 集:帕特里克·霍納最喜歡的定理
