本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點。
.jpg?w=300)
約翰·海因裡希·蘭伯特。圖片來源:公有領域,透過維基共享資源。
雙曲幾何的歷史充滿了雙曲的引言,我在本學期早些時候的數學史課上偶然發現了一句很精彩的引言。約翰·海因裡希·蘭伯特是一位1728-1777年間居住的瑞士數學家,他試圖證明平行公設,從而毫無疑問地確立歐幾里得幾何的真理,但最終卻證明了一些關於非歐幾里得幾何的非常奇特的事情。
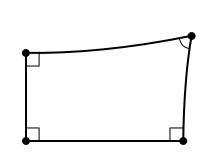
蘭伯特對幾何學的研究涉及到一個現在被稱為蘭伯特四邊形的圖形。(這個名字有些不恰當,因為10-11世紀的阿拉伯數學家伊本·海賽姆在蘭伯特之前700多年就使用了它們。)蘭伯特四邊形有四條邊和三個直角。
關於支援科學新聞業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞業 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和思想的具有影響力的故事的未來。
在高中幾何中,四邊形的角之和必須為 360°,但這個事實是基於假設歐幾里得平行公設。在歐幾里得蘭伯特四邊形中,第四個角也必須是 90°。蘭伯特想要證明第四個角必須是 90°,而無需使用平行公設。為了做到這一點,他探索了與第四個角的角度測量相對應的三種可能性:直角假設、鈍角假設和銳角假設。今天,我們會說這三個假設分別對應於歐幾里得幾何、橢圓或球面幾何以及雙曲幾何。蘭伯特發現,在第三個假設下,會發生一些令人困惑的事情:三角形的面積取決於其角之和,並且存在長度的“絕對”度量,也就是說,三角形不能在不扭曲其角的情況下變得更大。這些結果困擾了蘭伯特,他寫道*
“很容易看出,在第三個假設下,人們可以更進一步,並且在第二個假設下也可以找到類似的但截然相反的結果。但是,在很大程度上,我主要在第三個假設下尋找這樣的結果,以便看看是否會出現矛盾。從這一切可以清楚地看出,反駁這個假設絕非易事。我將引用更多結果,而不考慮它們在第二個假設下可以在多大程度上進行擴充套件,在必要時進行修改。”
“這些結果中最引人注目的是,在第三個假設下,我們將擁有每條線的長度、每個面的面積以及每個物理空間的體積的絕對度量。這駁斥了一些不明智的人認為幾何學公理的斷言,因為到目前為止,沒有人懷疑根本不存在絕對度量。這個結果有些精妙之處,讓人希望第三個假設是真的!”
“儘管有這樣的收穫,但我並不希望如此,因為這會導致無數的不便。三角函式表將無限大,圖形的相似性和比例性將完全消失,任何圖形都只能在其絕對大小中想象,天文學家將面臨困境,等等。”
“但所有這些都是由愛與恨決定的論據,它們在幾何學或整個科學中都不應該佔有一席之地。”
令人欽佩的是,蘭伯特認識到他對第三個假設的含義的反感並沒有使其無效。但有趣的是,蘭伯特發現絕對長度度量的想法如此令人反感——它就在我們眼皮底下。在球面上,對於任何給定的角集,只有一個大小的三角形。如果你想製作一個更大但具有相同角度的三角形,你必須在更大的球面上繪製它。一旦你確定了一個球體的大小,你就確定了所有三角形的大小。
今天,由於伯恩哈德·黎曼和許多其他人的努力,我們對幾何學的概念與蘭伯特的概念截然不同。蘭伯特試圖證明歐幾里得幾何是*唯一*真正的幾何。現在,我們有一種公理化的觀點:歐幾里得幾何是源於歐幾里得公理的真正幾何,但是如果我們改變這些公理,我們就會得到在不同上下文中有效的不同結果。球面幾何從一組不同的公理開始。現代數學家並不認為球面幾何是對的,而歐幾里得幾何是錯的,反之亦然。它們只是不同的公理系統。當蘭伯特將第三個假設與第二個假設進行比較時,他非常接近這種觀點,但他並沒有完全達到。他寫道
“回到第三個假設[銳角假設]。正如我們剛才所看到的,在這個假設下,每個三角形的三個角之和都小於 180 度,即兩個直角。但是,與 180 度的差值像三角形的面積一樣增加;這可以這樣表示:如果兩個三角形中的一個三角形的面積大於另一個三角形,那麼第一個三角形的角之和小於第二個三角形……。”
“我只想補充以下評論。完全類似的定理在第二個假設[鈍角假設]下成立,只是在第二個假設下,每個三角形的角之和都大於 180 度。超出的量始終與三角形的面積成正比。”
“我認為值得注意的是,如果我們將球面三角形而不是平面三角形,則第二個假設成立,因為它的角之和大於 180 度,並且超出的量也與三角形的面積成正比。”
“更令我震驚的是,我在這裡所說的關於球面三角形的內容可以獨立於平行線造成的困難來證明,並且僅僅假設每個穿過球體中心的平面都將其分成兩個相等部分的公理。”
“由此我幾乎可以得出結論,第三個假設在某種虛構的球面上成立。至少一定有什麼東西可以解釋這樣一個事實,即與第二個假設不同,它長期以來一直能夠抵制在平面上的反駁。”
雖然雙曲幾何不在“虛構的球面”上成立(假設他指的是半徑為虛數的球面),但蘭伯特的觀察非常敏銳。球面三角形的面積公式為 K2(a+b+c-180),其中 a、b 和 c 是三角形三個角的度量,K 是一個取決於球面半徑的常數。雙曲幾何中三角形的面積公式為 K2(180-a-b-c)。如果我們想象(哈!)第一個公式中的 K 是一個虛數,那麼它的平方是負數,我們就得到了第二個公式。(對於好奇的人來說,在這兩種情況下,K 都是包含三角形的曲面的曲率。曲率是我們現代幾何處理中的關鍵構建塊之一。)
蘭伯特差點取得突破,這將帶來幾何學的新時代,但這項榮譽最終歸於蘭伯特去世 50 多年後的亞諾什·波利亞伊和尼古拉·羅巴切夫斯基。儘管如此,他關於愛、恨和虛構球面的話語表明了熱情和創造力(以冷靜的邏輯為調和劑),這些熱情和創造力一直是數學中必不可少的,並最終導致了非歐幾里得革命。
* 蘭伯特的所有摘錄均來自 B.A. 羅森菲爾德的《非歐幾里得幾何史》的英文翻譯。粗體強調是我的。