本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點

一個可穿戴的、針織的 (5,3) 環面紐結。圖片來源:sarah-marie belcastro。
讓開,無限圍巾,你們根本不是無限的。(5,3) 環面紐結頸圈才是潮流。
對我來說,一月份聯合數學會議的亮點之一是數學纖維藝術環節。您可以在此處檢視我從該環節整理的幻燈片。在會議期間,聯合組織者莎拉-瑪麗·貝爾卡斯特羅作了關於她美麗的針織環面紐結和鏈環的演講。我在幻燈片中加入了一張它們照片,但想在這裡的部落格上分享更多關於它們的細節。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保未來能夠持續報道關於發現和塑造我們當今世界的想法的具有影響力的故事。
在數學中,紐結基本上就是現實世界中的紐結。你取一段繩子,以某種方式打結,然後將自由端連線在一起,使其沒有起點或終點。(我在去年的部落格文章中寫過關於紐結的文章,如果您想更深入地瞭解它們。)鏈環是任意數量的紐結放在一起。它們可能只是彼此相鄰,或者它們可能以某種有趣的方式纏繞在一起。

一個有三個元件的鏈環。這種配置稱為博羅梅安環,它很有趣,因為圖片中沒有兩個圓圈彼此連結,但是當所有三個放在一起時,你無法將它們拉開。圖片來源:公共領域,透過維基共享資源。
環面紐結和鏈環,貝爾卡斯特羅演講的主題,可以透過將繩子纏繞在環面或甜甜圈上製成。您可以將環面視為當您沿著另一個圓掃過一個圓時獲得的形狀,如下圖所示。
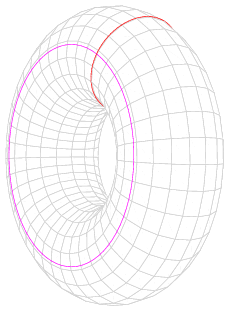
當您沿著粉紅色圓圈拖動紅色圓圈時,您會得到一個環面。圖片來源:Fropuff,透過維基共享資源。
我們可以將紅色圓圈和粉紅色圓圈,即穿過孔或圍繞孔纏繞的圓圈,分別視為環面上的兩個主要“方向”,類似於球體上的緯度和經度。
環面紐結或鏈環由它在兩個主要方向上纏繞多少次來定義。一個 (p,q) 環面鏈環* 穿過中心(沿著紅色圓圈)纏繞 p 次,圍繞孔(沿著粉紅色圓圈)纏繞 q 次。如果我們對 p 或 q 使用負數而不是正數,則描述是相同的,但紐結或鏈環在環面上以不同的方向螺旋纏繞。有關環面紐結的更多圖示,請檢視紐結圖譜。

一個以 3D 渲染的 (-7,3) 環面紐結。它圍繞環面的孔纏繞 3 次,穿過孔纏繞 7 次,但與 (7,3) 環面紐結的扭轉方向不同。圖片來源:Michiel Sikma,透過維基共享資源。
任何兩個整數 p 和 q 都可以定義一個環面鏈環。如果這些數字沒有公因數,則鏈環只有一個部分,因此我們稱之為紐結。如果它們確實有公因數,則鏈環有多個部分,例如這個 (4,2) 環面鏈環。(部分的數量與 p 和 q 共享的最大公因數相同。)
-Torus_Link.png?w=500)
一個 (4,2) 環面鏈環有兩個元件。圖片來源:公共領域,透過維基共享資源。
貝爾卡斯特羅既是數學家又是編織者,她已經擅長結合這兩個學科。她使用數學來理解和指導她的編織,並使用編織來視覺化複雜的數學物件。幾年前,貝爾卡斯特羅開始編織環面,使用對比鮮明的紗線在上面展示環面紐結。

淺綠色的 (5,3) 環面紐結,背景是深綠色的環面。圖片來源:sarah-marie belcastro。
當她繼續使用編織來探索數學時,她考慮過去掉環面,只編織紐結本身。當然,一種方法是編織一個細長的矩形,將其打結,然後將兩端縫合在一起。但這太容易了!相反,貝爾卡斯特羅想知道她是否可以進行編織,使紐結本質上是由編織建立的,而不是事後新增的。有一天,她將她的環形編織針(這些基本上是兩個端點,中間用一根長而柔韌的線連線)打成一個結,最終得到了一個針織的三葉結。

一個三葉結。圖片來源:公共領域,透過維基共享資源。
三葉結是除圓圈外最簡單的紐結,它也是一個 (3,2) 環面紐結。在成功編織三葉結後,貝爾卡斯特羅想知道她還可以建立哪些其他環面紐結和鏈環,並最終發現了一種遞迴演算法,用於正確地纏繞針頭以編織一些環面紐結。(具體來說,她的程式適用於 (nk+1, k) 環面紐結和 ((n+2)k-1,k) 環面紐結,適用於任何整數 n 和 k。)

一個針織的 (15,5) 環面鏈環。圖片來源:sarah-marie belcastro。
為了建立具有多個部分的環面鏈環,貝爾卡斯特羅首先使用她的演算法編織鏈環中的一個紐結,然後將其用作鏈環的下一個元件的基礎,她也使用她的纏繞演算法建立該元件。她不斷這樣做,直到她擁有所需的元件數量。因為她將針頭纏繞在之前的元件周圍以編織每個後續的紐結,所以成品具有所有內建的紐結性和鏈環性;無需在事後連線末端。

針織環面鏈環。從左到右,它們是 (4,2)、(6,4) 和 (8,6) 環面鏈環。每個鏈環都有兩個元件。圖片來源:sarah-marie belcastro。
貝爾卡斯特羅說,在編織完環面鏈環後,專案看起來一團糟。但她已經學會相信,當她從針頭上取下它並小心地將其展平時,她將最終得到一個漂亮、正確執行的環面鏈環。她通常僅出於其數學特性而製作紐結,但最近她發現,透過一些小的調整,她的 (5,3) 環面紐結可以製作成一個漂亮的頸圈。可穿戴的數學,勝出!
*環面紐結可以先標記任一方向。維基百科採用“圍繞孔”先出現的慣例,但貝爾卡斯特羅採用“穿過孔”先出現的慣例。這篇文章的原始版本在不同的地方使用了這兩種慣例。我已經更新了這篇文章以保持一致,使用貝爾卡斯特羅使用的慣例。如果您最終瀏覽到維基百科頁面,請記住它的環面紐結是使用相反的慣例標記的。