本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定代表《大眾科學》的觀點
今天在“我的最愛定理”節目中,我的聯合主持人凱文·克努森與紐約州立大學奧爾巴尼分校的數學家賈斯汀·柯里對話。他們在加拿大班夫國際研究站舉行的拓撲資料分析會議上進行了現場錄製。您可以在這裡收聽,也可以在kpknudson.com收聽。
柯里博士最喜歡的定理是柏拉圖立體的分類。這些是由全等正多邊形構成的五個凸多面體——四面體、立方體、八面體、十二面體和二十面體。四面體、八面體和二十面體分別由四個、八個和二十個等邊三角形構成,立方體由六個正方形構成,十二面體由十二個正五邊形構成。事實上,沒有其他多面體像它們一樣規則,這是一個由來已久但仍然美麗而引人注目的定理。
關於支援科學新聞事業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞事業 訂閱。透過購買訂閱,您將幫助確保未來能夠繼續報道關於塑造我們當今世界的發現和思想的具有影響力的故事。
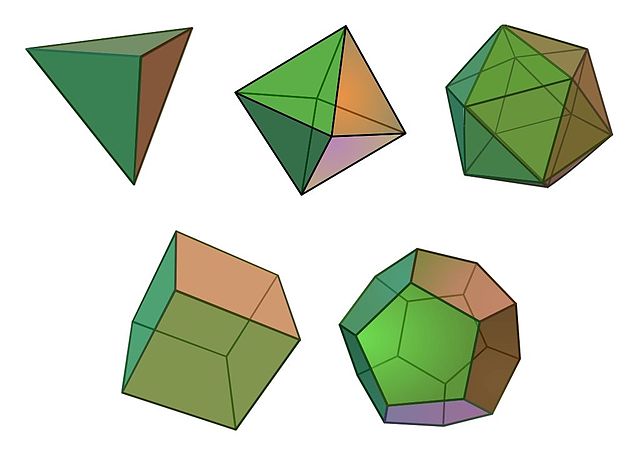
柏拉圖立體。頂行:四面體、八面體、二十面體。底行:立方體、十二面體。圖片來源: Максим Пе Wikimedia(CC BY-SA 4.0)
他們還談到了幾何學中的對偶性概念。對於任何多面體,你可以用面替換頂點,用頂點替換面,從而得到一個新的多面體。當您對柏拉圖立體執行此操作時,您會得到另一個柏拉圖立體作為其對偶。立方體是對八面體的對偶,十二面體是對二十面體的對偶,四面體是對自身的對偶。柯里博士非常喜歡這些立體及其對偶性,以至於他紋了關於它們的紋身。他有來自約翰內斯·開普勒的四面體紋身,一個來自藝術家alucinori的立方體-八面體對偶性設計,以及他自己設計的十二面體-二十面體對偶性紋身。如果您還沒有準備好達到那種程度的投入,凱文建議您不妨嘗試用摺紙製作這些立體,可以使用托馬斯·赫爾的著作《專案摺紙:探索數學的活動》。
在播客的每一集中,我們都會請嘉賓將他們的定理與某事物配對:食物、飲料、音樂、文學或生活中任何其他樂趣。對於他的配對,柯里博士選擇了字面意義上的——字面意義上的。他將柏拉圖立體與柏拉圖的《蒂邁歐篇》配對,柏拉圖在其中提出了他對宇宙本質的一些看法。他將四個柏拉圖立體——四面體、立方體、八面體和二十面體——與四個元素:火、土、氣和水聯絡起來。十二面體被認為是整個宇宙的形狀。您需要收聽這一集,才能聽到柯里博士關於立體中的對偶性概念如何在這些聯絡中得到反映的想法。
柏拉圖立體對於約翰內斯·開普勒的宇宙學也很重要。他1596年的著作《宇宙神秘論》包含了他的宇宙理論,即宇宙是一組巢狀的柏拉圖立體。雖然最終結果並非如此,但它看起來確實很酷。
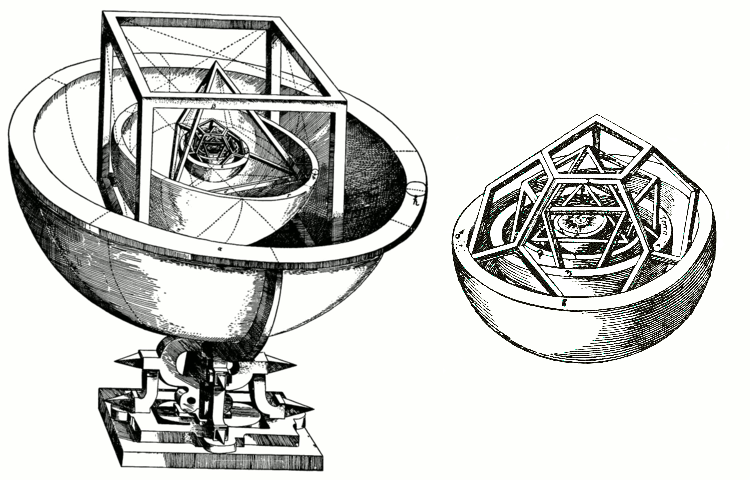
開普勒基於柏拉圖立體的太陽系模型,右側是內行星的細節。圖片來源: Mysterium Cosmographicum Wikimedia
您可以在 kpknudson.com 和 “統一的根源”找到更多關於本播客中介紹的數學家和定理的資訊,以及其他令人愉悅的數學內容。文字記錄在此處提供。您可以在 iTunes 和其他播客分發系統上訂閱和評論該播客。我們很樂意聽到聽眾的來信,請傳送郵件至 myfavoritetheorem@gmail.com。凱文·克努森的 Twitter 賬號是 @niveknosdunk,我的賬號是 @evelynjlamb。該節目本身也有一個 Twitter 賬號: @myfavethm 和一個 Facebook 頁面。請在下一次加入我們,學習另一個引人入勝的數學知識。
“我的最愛定理”節目往期回顧
第 0 集:您的主持人們最喜歡的定理 第 1 集:艾米·威爾金森最喜歡的定理 第 2 集:戴夫·裡奇森最喜歡的定理 第 3 集:埃米爾·戴維·勞倫斯最喜歡的定理 第 4 集:喬丹·艾倫伯格最喜歡的定理 第 5 集:杜薩·麥克達夫最喜歡的定理 第 6 集:繪里子·廣中 最喜歡的定理 第 7 集:亨利·福勒最喜歡的定理
