本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
在今天的“我最喜歡的定理”節目中,我的聯合主持人凱文有機會與科羅拉多大學博爾德分校的數學教授 Jeanne Clelland 進行了交談。他們去年夏天在塔夫茨大學的度量幾何和選區劃分小組會議上親自錄製了這期節目,我沒能參加。您可以在這裡或 kpknudson.com 收聽這期節目。
Clelland 選擇了 高斯-博內定理 作為她最喜歡的定理,我必須說她提出了一個非常有說服力的理由,以至於我正在認真考慮用高斯-博內定理來換取 我的單值化定理。我們一直在我們的 Twitter 和 Facebook 頁面上使用高斯-博內定理作為我們的橫幅圖片,所以 Clelland 博士確保我們沒有做任何虛假宣傳真是太好了!
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您將幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和思想的具有影響力的故事。
高斯-博內定理真是一個奇蹟。就像我最喜歡的定理和 Emille Davie Lawrence 最喜歡的定理 一樣,它是關於二維表面的。雖然有一些推廣,但 Clelland 博士專注於緊湊的二維表面的情況,這意味著它們是有限且無穿孔的,就像甜甜圈的釉面或椒鹽捲餅的表面。
高斯-博內定理指出,這種表面的總曲率,或曲率在表面上的積分,僅取決於它擁有的孔的數量,也稱為它的虧格。一個球體的虧格為 0,一個環面或甜甜圈的虧格為 1,以此類推。
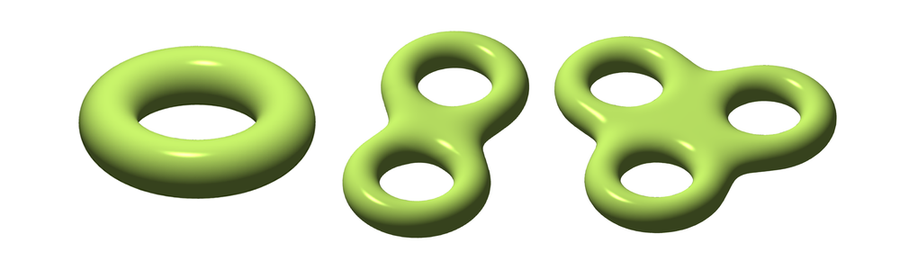
從左到右:虧格為 1、2 和 3 的表面的圖片。圖片來源:基於 Oleg Alexandrov 的圖片
表面的曲率是一種量化表面彎曲程度的方法。如果在給定點,表面上的每條線都從切平面向同一方向彎曲(就像球體上的線一樣),那麼該點就具有正曲率。如果表面上的一些線在一個方向彎曲,而另一些線在另一個方向彎曲(就像馬鞍從前向後向上彎曲,從一側到另一側向下彎曲一樣),則該表面在該點具有負曲率。如果表面沿著某條線沒有彎曲,例如圓柱體的“高度”方向,則它具有零曲率。當表面幾乎平坦時,曲率接近於零,而當表面非常彎曲時,曲率遠離零。因此,沙灘球在任何給定點的曲率都比彈珠低。

從左到右:具有負曲率、零曲率和正曲率的表面。圖片來源:Jhausauer Wikimedia
曲率可以在表面上變化,但高斯-博內定理指出,它總是以某種方式平衡,這種方式僅取決於其虧格。當我進行研究時,我研究的表面具有恆定曲率,因此高斯-博內定理意味著我可以僅根據表面的虧格來確定表面的面積。Clelland 博士還指出了高斯-博內定理與球體上三角形的面積公式之間的關係。
Clelland 決定避開明顯的(但美味的)甜甜圈或百吉餅與高斯-博內的搭配,而是建議焰火表演和 柴可夫斯基的《1812序曲》。您可以收聽這期節目,瞭解它們為何與高斯-博內定理如此相配。
Clelland 是 《從弗雷內到嘉當:移動標架法》 一書的作者,這是一本關於微分幾何的高階本科或研究生水平的教科書。您可以在 kpknudson.com 和 Roots of Unity 上找到有關此播客中出現的數學家和定理以及其他令人愉悅的數學知識的更多資訊。 此處提供文字稿。您可以在 iTunes 和其他播客傳送系統上 訂閱和評論該播客。我們很樂意聽到聽眾的來信,所以請傳送郵件至 myfavoritetheorem@gmail.com 聯絡我們。Kevin Knudson 的 Twitter 賬號是 @niveknosdunk,我的賬號是 @evelynjlamb。該節目本身也有一個 Twitter 賬號:@myfavethm 和一個 Facebook 頁面。請在下次加入我們,學習另一個引人入勝的數學知識。
“我最喜歡的定理”節目回顧
第 0 集:您的主持人們最喜歡的定理 第 1 集:Amie Wilkinson 最喜歡的定理 第 2 集:Dave Richeson 最喜歡的定理 第 3 集:Emille Davie Lawrence 最喜歡的定理 第 4 集:Jordan Ellenberg 最喜歡的定理 第 5 集:Dusa McDuff 最喜歡的定理 第 6 集:Eriko Hironaka 最喜歡的定理 第 7 集:Henry Fowler 最喜歡的定理 第 8 集:Justin Curry 最喜歡的定理 第 9 集:Ami Radunskaya 最喜歡的定理 第 10 集:Mohamed Omar 最喜歡的定理
