本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
在我們的播客“我最喜歡的定理”這一集中,我的聯合主持人凱文·克努森和我很高興與來自中國深圳南方科技大學的 Jana Rodriguez Hertz 交談。您可以在此處或在 kpknudson.com 上收聽該節目,其中還有一份文字稿。
羅德里格斯·赫茲博士選擇在節目中談論史蒂芬·斯梅爾的馬蹄形對映。但首先她談到了麵條。她拍攝了一段影片,記錄了她校園食堂的一位廚師製作麵條的過程。廚師拉伸麵條,將麵條自身摺疊起來,然後再拉伸,重複幾次步驟,然後將麵條扔進鍋裡。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過 訂閱來支援我們屢獲殊榮的新聞工作。透過購買訂閱,您將有助於確保關於塑造我們當今世界的發現和想法的具有影響力的故事的未來。
這個過程很像馬蹄形對映。馬蹄形對映是從一個正方形到它自身的一個函式。首先,您透過在一個方向上擠壓並在另一個方向上拉伸來使正方形變形,這樣您就得到一個長而窄的條帶,其面積與原始正方形相同。現在,您將條帶摺疊成馬蹄形,使其 1/3 位於正方形的 1/3 中,1/3 位於另一個正方形的 1/3 中,中間的 1/3 形成馬蹄形的彎曲部分。出於此對映的目的,我們將丟棄中間的 1/3,即沒有回到原始正方形的部分。在下圖所示,正方形的左 1/3 已對映到正方形的底部 1/3,正方形的右 1/3 已對映到正方形的頂部 1/3。(在播客節目中,羅德里格斯·赫茲博士描述了該圖中地圖的旋轉版本。這個想法是一樣的。)
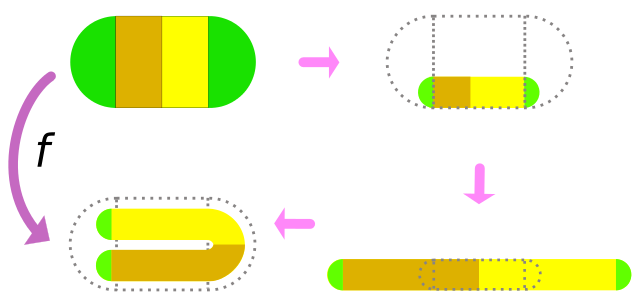
斯梅爾馬蹄形對映的示意圖。圖片來源:SyntaxError55 Wikimedia(CC BY-SA 3.0)
如果您只執行一次對映,那麼它並沒有那麼令人印象深刻,但如果您像廚師做麵條那樣執行一次變換,然後再執行一次又一次,您就會開始得到一些很酷的東西,而這種酷行為是羅德里格斯·赫茲博士最喜歡的定理。大多數點最終都會被丟棄,因為它們在某個時間被卡在馬蹄形的彎曲部分中,但留在正方形中的部分會被拉伸成康託集的麵條狀版本。(在此處閱讀有關康託集的更多資訊。)

建立康託集的無限過程的七次迭代。圖片來源:127rect Wikimedia
您還可以想象反向執行對映。不是正方形的頂部 1/3 對映到左 1/3,底部對映到右 1/3,而是得到正方形的左 1/3 對映到頂部 1/3,右 1/3 對映到底部 1/3。您可以問,無論向前還是向後,是否會有任何點永遠留在正方形中,而且確實有一些。永遠停留的點,也稱為不變集,形成一個名為康託塵埃的空間。

康託塵埃是兩個康託集的乘積,就像平面是兩條直線的乘積一樣。圖片來源:Solkoll Wikimedia
正如羅德里格斯·赫茲博士所描述的那樣,馬蹄形對映生動地說明了從一個相當簡單的系統中產生的混沌行為。混沌的標誌之一是混沌系統對初始條件非常敏感,馬蹄形對映也適用。無論兩個點彼此有多近,最終它們的行為都將完全不同。事實上,正如她所提到的,您實際上可以透過記錄它在此對映的迭代下所去的位置來完全且唯一地描述一個點,這個想法與所謂的符號動力學相關。羅德里格斯·赫茲博士還提到了一個名為帳篷對映的對映,這是另一個具有混沌行為的簡單系統。您可以在此處閱讀更多相關資訊。
她還提到了馬蹄形對映與一個名為符號動力學的領域的聯絡。符號動力學的基本思想是,您可以使用有限數量的字母或數字來編碼系統中經歷變換的點的行為。在馬蹄形對映的情況下,她描述瞭如何用 0 和 1 的序列來描述不變集中的每個點,它們代表了它在每個步驟中(向前和向後)所處集合的哪個部分。
.JPG?w=450)
羅德里格斯·赫茲博士與斯梅爾馬蹄形對映的同名者史蒂芬·斯梅爾合影。圖片來源:Jana Rodriguez Hertz
在播客的每一集中,我們都會請嘉賓將他們的定理與某個事物配對。羅德里格斯·赫茲博士出生於阿根廷,在搬到中國之前在烏拉圭工作了很多年,她即興發揮了一個想法,即馬蹄形對映中的一個點完全由它的路徑決定,並談到了這個想法如何在她的生活中產生共鳴。您必須收聽這一集才能瞭解完整的故事。我認為有趣的是,她和艾米·拉敦斯卡婭(她與我們談論了伯克霍夫遍歷定理)都來自動力系統領域,他們都在哲學上探討了如何將他們的定理視為隱喻。
您可以在 Twitter 上關注羅德里格斯·赫茲博士。您可以在kpknudson.com和“統一之根”中找到有關此播客中出現的數學家和定理的更多資訊以及其他令人愉悅的數學資訊。 此處提供文字稿。您可以在 iTunes 和其他播客傳輸系統中訂閱和評論該播客。我們很樂意收到聽眾的來信,因此請透過myfavoritetheorem@gmail.com給我們留言。凱文·克努森在 Twitter 上的賬號是@niveknosdunk,而我的賬號是@evelynjlamb。該節目本身也有一個 Twitter 動態:@myfavethm和一個Facebook 頁面。下次加入我們,學習另一件引人入勝的數學知識。
“我最喜歡的定理”之前的內容
第 0 集:您主持人的最愛定理 第 1 集:Amie Wilkinson 最喜歡的定理 第 2 集:Dave Richeson 最喜歡的定理 第 3 集:Emille Davie Lawrence 最喜歡的定理 第 4 集:Jordan Ellenberg 最喜歡的定理 第 5 集:Dusa McDuff 最喜歡的定理 第 6 集:Eriko Hironaka 最喜歡的定理 第 7 集:Henry Fowler 最喜歡的定理 第 8 集:Justin Curry 最喜歡的定理 第 9 集:Ami Radunskaya 最喜歡的定理 第 10 集:Mohamed Omar 最喜歡的定理 第 11 集:Jeanne Clelland 最喜歡的定理 第 12 集:Candice Price 最喜歡的定理 第 13 集:Patrick Honner 最喜歡的定理 第 14 集:Laura Taalman 最喜歡的定理 第 15 集:Federico Ardila 最喜歡的定理 第 16 集:Jayadev Athreya 最喜歡的定理 第 17 集:Nalini Joshi 最喜歡的定理 第 18 集:John Urschel 最喜歡的定理 第 19 集:Emily Riehl 最喜歡的定理 第 20 集:Francis Su 最喜歡的定理