本文發表於《大眾科學》的前部落格網路,僅反映作者的觀點,不一定反映《大眾科學》的觀點
前幾天,我在我最喜歡的部落格之一數學教授語錄上看到一句話,有點讓我震驚:“宇宙中任何數的 log log 值實際上都小於 5。”
如果您的高中數學知識有點模糊,那麼數的對數(logarithm 的縮寫)基本上就是它的數量級。目前尚不清楚這位匿名數學教授說的是以 10 為底的對數還是自然對數,還是他或她偏愛的其他對數,但這其實並不重要。 想法是一樣的。
更技術性地說,如果 y=log(x),並且我們討論的是以 10 為底的對數,這意味著 y 是使 10y 等於 x 的數。所以 log(10)=1,log(100)=2,因為 10^1=10,10^2=100。* 對數是指數函式的反函式。 我認為它是一種“扁平化”函式:介於 10 和 100 之間的所有數的對數都在 1 和 2 之間,介於 100 和 1000 之間的所有數的對數都在 2 和 3 之間。 差異被扁平化了。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。 透過購買訂閱,您將幫助確保有關塑造我們當今世界的發現和思想的具有影響力的故事的未來。
那麼,一個數的 log log 值是數量級的數量級。 它使數字更加扁平化。 正如指數增長速度快於乘法(並且 向上箭頭 增長速度快於指數),log 增長速度慢於乘法,log log 增長速度慢於 log。 雖然 log 10 和 log 100 相差 1,但它們的 log log 值僅相差 0.3。 直到 10,000,000,000,log log 值才達到 1。
那麼,宇宙中任何數的 log log 值都小於 5 嗎? 現在,教授所說的底數可能很重要。 如果教授指的是以 10 為底的對數,那麼任何小於 10105 的數(即 1 後面跟 100,000 個零)的 log log 值都小於 5。 我不知道您怎麼樣,但在我的日常生活中,我並不經常需要這麼大的數字。
但是,我猜這位好教授可能指的是自然對數,或者 以 e 為底的對數,因為那是數學家通常使用的對數。 我將把它寫成“ln”以避免歧義,儘管我會注意到,在我的腦海裡,我仍然把它發音為“log”。
即使是以 e 為底數,ln ln 值為 5 的數也大得難以置信。 數 ee5 大約是 3x1064,因此任何小於該數的數的 ln ln 值都小於 5。 我很少甚至只是轉瞬即逝地想到這麼大的數字。 作為參考,宇宙中大約有 1080 個原子。 如果我們經常談論所有原子,我們就需要一個 ln ln 值為 5.2 的數。 向上舍入到 googol 也不會改變太多:現在我們大約是 5.4。
思考 log log 的增長速度有多慢以及它使數軸扁平化的程度,我開始思考我在微積分第二學期第一次遇到的一些無窮級數,它們仍然讓我著迷。 首先,是調和級數
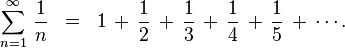
調和級數是發散的,這意味著即使項變得越來越小,總和也是無窮大的。(我不會剝奪您弄清楚它為什麼是無窮大的樂趣,但我會給您一個提示:考慮對項進行分組,看看您是否可以將所有組都變得大於 1/2。)
儘管調和級數是發散的,但它的發散速度非常慢。 本·奧林報告說,googol 項之後的總和約為 230。 換句話說,透過微小的分數向上計數是達到無窮大的一種低效方法。
這與 log log 有什麼關係呢? 嗯,有一個發散級數,它比調和級數更慢地逃逸到無窮大:從 2 到無窮大的 1/n(ln(n)) 的和。(為什麼要從 2 到無窮大而不是從 1 開始? 如果我們試圖包含 n=1 項,我們就會被除以 ln(1)(也稱為 0)所造成的災難所吞噬。)
讓我們思考一下級數 ∑1/n(ln(n)) 正在發生什麼。 每一項都小於調和級數的對應項,調和級數是發散的。 另一方面,它大於 1/n2 的對應項,而 1/n2 是收斂的。
幸運的是,我們可以引入一些積分來使我們自己確信 ∑1/n(ln(n)) 確實是發散的。 函式 1/x 有點像序列 1/n。 該函式只是在序列的步驟之間進行插值。

函式 y=1/x 的圖以及高度均為 1/n 的步驟(對於 n=1、2、3 等)。 函式 1/x 曲線下的面積被深色陰影覆蓋,步驟下的面積被淺色陰影覆蓋。 影像使用 Desmos 建立。
函式 y=1/x 的積分(上面曲線下的面積)與級數 ∑1/n 的和相關:要麼兩者都是有限的,要麼兩者都是無限的。 這為我們提供了一種不太有趣的方法來證明調和級數是發散的:1/x 的積分是 ln(x),它會任意增長,因此從 x=1 一直到無窮大的曲線下面積是無限的。
一般來說,將無窮級數與連續函式的積分進行比較是瞭解和是否有限或無限的好方法。 對於級數 ∑1/n(ln(n)),我們將它與函式 y=1/x(ln(x)) 進行比較。 如果我們可以弄清楚 1/x(ln(x)) 的積分是否有限,我們就會知道該級數是否收斂。
這裡的細節並不重要,但事實證明 1/x(ln(x)) 的積分是 ln(ln(x)),我們心愛的 log log。 再次,一個數的 log log 值可以達到的值沒有界限,因此從 2 到無窮大的 1/x(ln(x)) 的積分和從 2 到無窮大的 1/n(ln(n)) 的和都是無限的。
如果您認為調和級數發散得很慢,那麼您會被 ∑1/n(ln(n)) 震驚到。 在 googol 項之後,調和級數的和為 230。 1/n(ln(n)) 的前 googol 項的和約為 ln(ln(one googol)),您可能還記得它是 5.4。 如果您想透過步長為 1/n(ln(n)) 的步子一直走到 230,您將需要走很長一段時間。
但是等等,還有更多!(或者更少,取決於您如何看待它。) 宏偉的鏈式法則 使我們能夠構建一整套都趨於無窮大的級數,每個級數都比上一個級數更慢。 我們只需開始堆疊對數即可。

它很快就變得很荒謬。 ∑1/n(ln(n))(ln(ln(n))) 的和有點像 1/x(ln(x))(ln(ln(x))) 的積分。 該積分是 ln(ln(ln(x))),因此 ∑1/n(ln(n))(ln(ln(n))) 一直到 googol 的和約為 1.69。
級數 ∑1/n(ln(n))(ln(ln(n)))(ln(ln(ln(n)))) 的增長速度甚至更慢。 我們與之比較的函式 1/x(ln(x))(ln(ln(x)))(ln(ln(ln(x)))) 的積分是 ln(ln(ln(ln(x))))。 在 googol 處,該值略高於一半。
我們可以整天不斷新增對數,並獲得發散速度越來越慢的級數。 我正在掩蓋的一個奇怪之處是找到每個級數或積分的正確起點。 您不想意外地除以 0 或嘗試取負數的自然對數,因此您必須比上一個級數稍晚開始每個級數,以避免這些複雜情況。
我想不出任何實際理由讓我想要找到從 n=16 開始的 ∑1/n(ln(n))(ln(ln(n)))(ln(ln(ln(n)))),但我認為思考這些痛苦地緩慢的通往無窮大及更遠的路程很有趣。 畢竟,生活在於旅程,而不在於目的地。
*如果您是在新版本的《大眾科學》網站上檢視此帖子,則指數的格式可能不正確。 頁面頂部可能會有一個選項,可以在舊版本的網站上檢視它。
