本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
瑪麗安·米爾扎哈尼於7月14日去世。她是一位傑出的數學家,並在2014年成為首位女性和首位伊朗人獲得著名的菲爾茲獎時一舉成名。她年僅40歲。她本應擁有更美好的未來。 她的去世是數學界的巨大損失。
米爾扎哈尼的訃告, 包括我寫的那篇, 傾向於提及她對雙曲幾何和檯球的興趣。這些文章中不太清楚的是這兩個領域是如何聯絡起來的。簡而言之,我們可以透過將檯球桌展開成可以支援雙曲幾何的表面來連線這兩個領域。
雙曲幾何是研究自然幾何形狀處處呈馬鞍狀的曲面的學科。區域性來看,二維物體,如沙灘球或百吉餅的表面,可以具有三種不同的幾何形狀之一:正曲率(像球體一樣彎曲)、負曲率(像馬鞍或品客薯片一樣彎曲)或平坦(像一張紙或桌面)。此外,曲面可以根據整個物體的“自然”幾何形狀型別進行分類。一個放在我們真實三維世界中的百吉餅,有些地方像球狀,有些地方像馬鞍狀,但作為一個抽象的表面,它的“自然”幾何形狀實際上是平坦的。看到這一點的其中一種方法是,你可以透過將邊緣粘合在一起,用一張平紙構建一個類似百吉餅的形狀,或環面。有關更多資訊,請參閱這篇關於環面的文章。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞事業: 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和想法的具有影響力的故事。
沒有孔洞的物體,如沙灘球,自然是正曲率的(也稱為球面幾何),而有很多孔洞的物體,如椒鹽捲餅,則具有自然的負曲率(也稱為雙曲幾何)。米爾扎哈尼研究了有很多孔洞的曲面。
這些曲面通常來自檯球桌。儘管數學家關心各種不同形狀的檯球桌,但我們不妨從矩形桌子開始,看看我們如何從一個平面矩形(檯球在上面彈跳)到一個曲面,在本例中是一個環面。我在一篇關於我最喜歡的空間之一的文章中寫到了這一點,沿狹縫粘合的兩個環面,所以這個解釋是從那篇文章改編而來的。
數學臺球是理想化的。沒有摩擦會減慢它們的速度。 與具有一定面積的球不同,一個點沿直線運動,直到它撞到桌子的邊緣,此時它與邊緣發生完全彈性碰撞,並沿另一個方向繼續前進。(入射角等於反射角,因此如果它正面撞擊檯球桌的邊緣,它將沿同一方向反射回來。如果它以 30° 角撞擊,它將以 30° 角彈開。)
所有這些彈跳和方向改變使得跟蹤軌跡變得複雜,因此數學家採用了一個巧妙的技巧來簡化他們的問題:他們展開桌子。當球撞到邊緣時,我們不是反射球的軌跡,而是反射桌子,球繼續不受阻礙地前進。這樣,方向永遠保持不變。為了瞭解這在矩形中是如何工作的,我們將跟蹤一個點來看看會發生什麼。
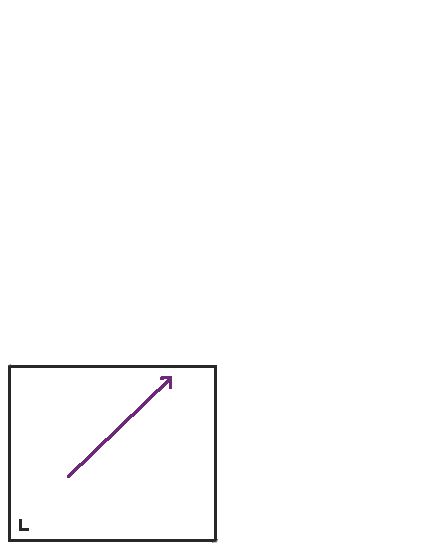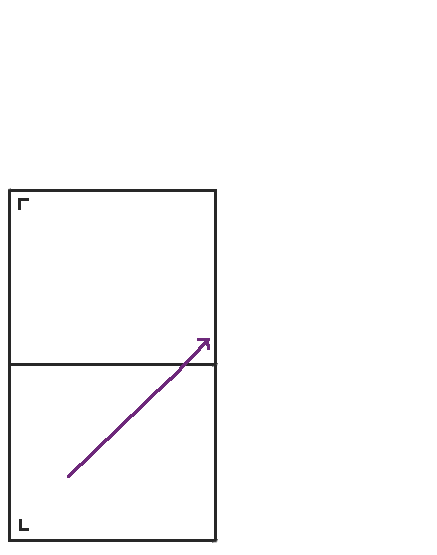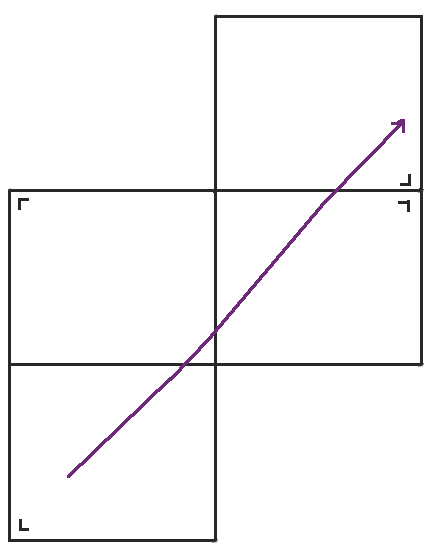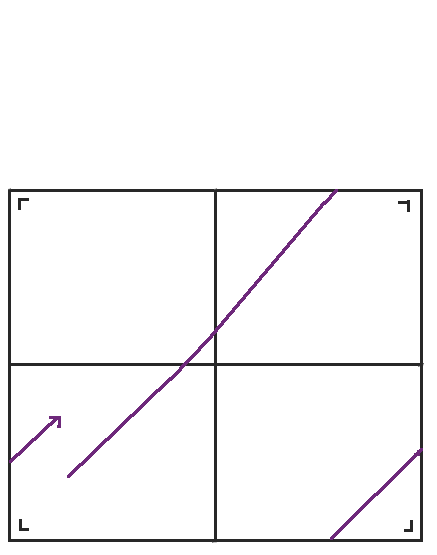
首先,我們從在一個矩形中向東北方向移動開始。我在左下角用一個小 L 標記了矩形,以便我們在展開桌子時跟蹤桌子的方向。
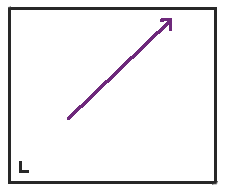
當我們到達矩形的頂部時,我們不是彈回,而是將桌子沿頂部反射,然後點繼續前進。
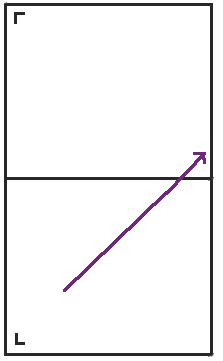
當我們到達桌子的右側時,我們將桌子沿右側反射並繼續前進。

當我們到達那個桌子的頂部時,我們再次反射。
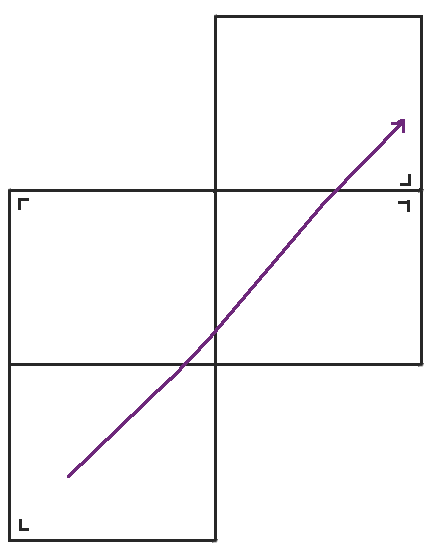
當我們到達右側時,我們可以再次反射桌子,但是左下角的桌子與我們將得到的桌子具有相同的方向,所以我們不妨再次跳回到左下角的桌子。當我們稍微重新排列桌子時,我們得到了我們熟悉的環面,一個頂部粘到底部,左側粘到右側的矩形。

這是整個過程的 gif 動畫。
透過這種方式,我們從矩形上的檯球運動過渡到環面上的直線流。我在研究生院看過幾次這個展開演示,我感覺非常自信我理解了它。但是矩形是一個簡單的形狀。最後,它展開成一個自然平坦的表面。我是否可以執行這個展開程式並獲得一個自然雙曲的表面? 在下一篇文章中,我將寫下當我嘗試展開五邊形檯球桌時發生的事情。