本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
這一切都始於粗糙的斜裁滾邊。斜裁滾邊是用沿織物對角線(“斜紋”)裁剪的布條製成的,使其比平行於紋理裁剪的布條更具彈性和延展性。它的柔韌性使其非常適合包邊彎曲邊緣。不幸的是,我為最近的專案——給新生嬰兒製作圍兜——購買的斜裁滾邊是一種粗糙的滌綸。我沒有嘗試尋找顏色搭配良好的棉質滾邊,而是決定用剩下的布料自己製作。
製作斜裁滾邊的一種方法是將幾條斜紋布條裁剪下來,縫合在一起,然後將它們穿過您方便的斜裁滾邊器。這種方法是最直接的方法,但它也有缺點。您必須一次縫製許多接縫,並且最終會得到一些煩人的小布料碎片,這些碎片真的不值得縫合在一起而被扔掉。

關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
幾年前,一位朋友分享了一個製作連續滾邊的驚人教程。我使用過這個教程幾次,它總是讓我感到驚歎。連結中有完整的詳細資訊,但主要思想是,您不是裁剪對角線布條然後再縫合在一起,而是在裁剪出來之前先將它們縫合在一起。
您從一塊正方形的布料開始,然後沿著其中一條對角線裁剪,並將頂部縫合到底部。
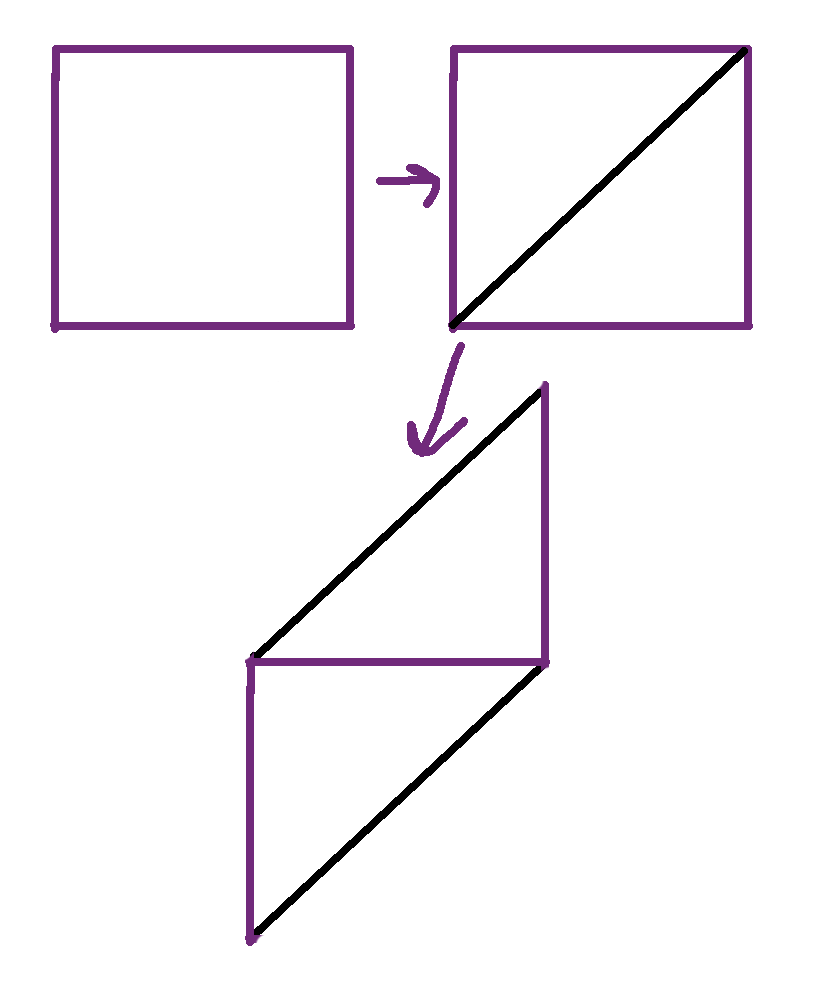
此時,您可以裁剪一堆長度相同的斜紋布條,然後將它們逐個縫合在一起,但該教程仍然更聰明:您將左右兩側縫合在一起。如果您將它們縫合得完美對齊,您最終只會得到一堆布料環。相反,您稍微偏移它,使其在您完成時自然地流動成一條長布料。
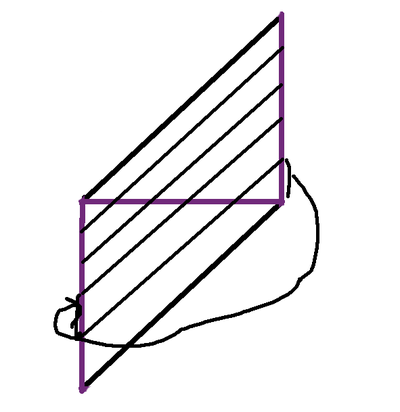
我已經使用過這個教程幾次了,它總是讓我感到高興。當您開始裁剪並最終得到您想要的斜紋布條時,這幾乎是神奇的。最近一次我製作它時,我專注於這個過程的拓撲結構。當您將頂部縫合到底部並將左側縫合到右側時,您正在製作一個奇怪的環面。由於側面的偏移,它與環面的漂亮矩形圖片不太一樣,但這給了我一個想法:我可以先製作奇怪的環面,然後沿對角線裁剪以裁剪出布條嗎?我必須嘗試一下!
首先,我從布料上裁剪出一個正方形,並在上面畫出對角線,以幫助我對齊我的工作。

然後我縫製了第一條接縫,將正方形變成一個管狀。
.jpg?w=400)
然後是困難的部分,在偏移的情況下將左側縫合到右側。

我成功了!我最終得到一個環面,由於偏移,它有一個孔。

在這一點上,理論上,我可以開始裁剪,並最終繞著整個環面進行。
.jpg?w=400)
成功了!

我很激動它成功了,但數學家很難滿足。一旦我們解決了一個問題,我們就想看看是否可以簡化證明或推廣定理。我的斜裁滾邊冒險也不例外。奇怪的環面方法很有趣,但我可以做些什麼來避免沿著偏移縫合邊緣嗎?我可以使用一個真正的環面而不是一個奇怪的環面嗎?
為了弄清楚如何解決這個問題,我必須思考一下為什麼我一開始就不能縫製一個規則的環面。原因是如果我這樣做,我最終會得到幾個斜裁滾邊環,而不是一條長條。在更深層次上,問題是斜裁滾邊以相對於織物紋理成 45° 角裁剪。將織物視為一張方格紙,斜裁滾邊的斜率為 1。我可以在方格紙上繪製它,方法是將頂部/底部和左側/右側分成相同數量的部分,然後連線這些點。我將得到與頂部和底部分割數一樣多的環。
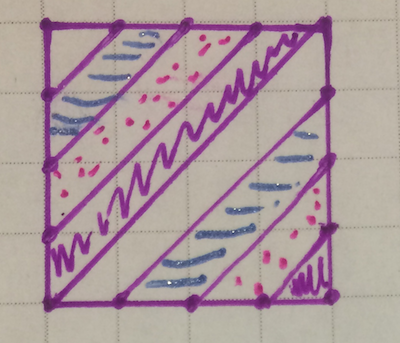
如果我將環面的頂部/底部和側面都分成四部分,我將得到四條單獨的布條。
一般來說,在環面上,如果我將頂部/底部分成m部分,並將左側/右側分成n部分,我將得到gcd(m,n)條單獨的布條。如果 m 和 n 沒有公因數,我將只得到一條布條,正如所期望的那樣。
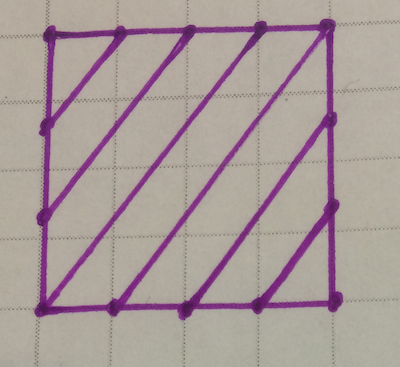
如果我將頂部/底部分成四部分,並將側面分成三部分,我將只得到一條布條。不相信我?用您的眼睛或手指跟隨這條布條。
唯一的問題是我不再製作斜裁滾邊了。我正在製作非斜裁滾邊。我的滾邊的斜率將不再是 1,而是一些接近 1 的分數。如果我將底部分成m部分,並將側面分成n部分,則斜率將為m/n。
現實世界有多在意我的斜裁滾邊不是完全斜裁的?縫紉是一種近似的嘗試,所以我認為現實世界不會太在意我的斜裁布條是否不夠完美。受到鼓舞,我決定放手一搏。
我計算了數字,並確定為了獲得 2 英寸寬的斜裁布條,我需要從 24 英寸的正方形布料開始,並將頂部和底部均分為九等份,並將側面均分為八等份。然後我連線了這些點。

將布料的正面朝裡,我將頂部縫合到底部,並將左側縫合到右側。我得到了一個環面,上面纏繞著一條長螺旋線。

然後我在上面剪了一個小孔,開始裁剪。

成功了,我最終得到一個 288 英寸長的幾乎是斜裁的布料環,我將其剪開做成一條長條。我特別喜歡注意到這個小點,原始正方形的角在這裡匯合在一起,並向我展示了一個小直角三角形,其直角邊長之比為 8:9。在典型的斜裁滾邊中,這個點將是一個等腰直角三角形。

令我驚訝的是,當我使用非斜裁滾邊時,我確實注意到它感覺不如真正的斜裁滾邊那麼靈活。我確信,如果我在每一側新增更多的分割,例如將斜率從 9/8 更改為 11/10 或 24/23,非斜裁滾邊的作用將越來越像真正的斜裁滾邊。但我的 9/8 斜裁滾邊完成了這項工作。(如果我可以這麼說,非常可愛。)

我的環面方法不是製作斜裁滾邊的最佳方法。這項榮譽屬於我最初進行實驗所依據的教程。如果您只是想以一種巧妙、高效的方式製作一些斜裁滾邊,您應該使用那個教程。但我的實驗幫助我更深入地瞭解了斜裁滾邊以及環面的幾何形狀和動力學。
這個專案也讓我思考縫紉中隱藏的數學。縫紉中有很多顯而易見的數學:測量布料、紙樣放碼、計算縫份。但縫紉中的數學遠比這些技能更深入。當您深入研究時,縫紉是應用幾何學。您正在使用扁平的布料來近似複雜曲面的曲率。女裁縫和其他縫紉師在應用幾何學方面的研究並沒有得到太多認可,這可能是因為傳統上“女性化”的活動不被認為是很有數學性的。當然,我們這些縫紉或製作鉤編雙曲面飛機或克萊因四次曲線的人更清楚!
