本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
安娜麗莎·克蘭內爾去藝術博物館時帶著筷子。她不是特別餓或準備過度;她用筷子來弄清楚如何欣賞藝術。
克蘭內爾是賓夕法尼亞州蘭開斯特市富蘭克林與馬歇爾學院的一位數學家,她研究數學透視,並將她的研究應用於藝術世界。她不僅撰寫關於藝術家如何運用透視的文章,還撰寫關於觀眾如何運用透視以不同方式欣賞藝術的文章。
在2014年《數學地平線》雜誌的一篇文章(pdf格式,也可在《2015年最佳數學寫作選集》,米爾恰·皮蒂奇編輯中找到)中,她與合著者馬克·弗朗茨和富美子·弗塔穆拉一起探討了15世紀和16世紀德國藝術家阿爾布雷希特·丟勒的著名版畫《書房裡的聖哲羅姆》中神秘的桌子。
支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和思想的有影響力的故事的未來。

阿爾布雷希特·丟勒的《書房裡的聖哲羅姆》。公共領域,透過維基共享資源。
這部作品是藝術中數學透視的早期範例,但一些評論家貶低了丟勒的技巧。紐約大都會藝術博物館的前館長小威廉·米爾斯·艾文斯將其描述為“最奇怪的梯形形狀”,並聲稱它甚至與地面不水平。克蘭內爾和她的合著者表示,這是一個透視問題。他們寫道:“令人驚訝的是,這些問題的答案不僅取決於丟勒在500年前做了什麼,還取決於艾文斯在1938年做了什麼。而且,正如我們將要展示的那樣,它取決於你,讀者,今天在觀看《聖哲羅姆》時做了什麼。”
克蘭內爾和她的合著者描述瞭如何在《書房裡的聖哲羅姆》中使用直線來確定觀眾應該站在哪裡才能從丟勒可能想要的透視角度觀看這幅畫,從而將桌子看作正方形而不是梯形。對於那幅特殊的版畫來說,合適的觀看位置比大多數人自然站立的位置更靠近畫面,並且更靠右。他們寫道:“艾文斯在桌子上看到的奇怪之處不是因為丟勒錯了,而是因為艾文斯錯了,字面意思是:他站在了錯誤的位置觀看!”
二月份,我有幸與克蘭內爾一起去了楊百翰大學藝術博物館,她與我分享了她的一些秘訣。(楊百翰大學藝術博物館通常不允許拍照,因此我感謝他們為我們破例。)
在透視藝術中,繪畫中代表現實世界中平行線的線條——例如,鐵軌或桌子的相對兩側——在畫布上相交於所謂的消失點。這些消失點是確定觀看繪畫的最佳位置的關鍵。
找到繪畫的消失點並因此確定最佳觀看位置的最明顯方法是將尺子直接放在繪畫中“平行”的線條上,但令人震驚的是,大多數博物館都不贊成這種做法。這就是筷子派上用場的地方。

圖片:伊芙琳·蘭姆。
克蘭內爾站在一件藝術品前,閉上一隻眼睛,將筷子放在她面前,使它們與藝術品中代表現實世界中平行線的線條對齊。筷子看起來相交的地方就在這些線條的消失點前面。對於只有一個消失點的藝術品,觀眾應該直接站在該點的前面。觀看距離可以透過試錯法或一些帶有正方形的巧妙幾何學來確定。
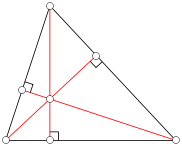
一個說明三角形垂心的圖示。每條紅線都是三角形的一條高線。圖片:公共領域-自制,透過維基共享資源。
對於有兩個消失點的藝術品,最佳觀看點位於連線兩個消失點的半圓上的某個位置。對於有三個消失點的藝術品,確定最佳觀看點稍微複雜一些。它位於三個半球的交點,每個半球都有兩個消失點作為直徑。等效地,它位於頂點為消失點的三角形的垂心前面(三角形的垂心是三角形三條高線的交點,如右圖所示)。有關如何在藝術中找到觀看點的更完整描述,請檢視克蘭內爾和弗朗茨的《視角:藝術中的數學透視和分形幾何》。
除了給我一種在博物館裡顯得古怪的方法外,克蘭內爾的技術還幫助我理解為什麼有些畫作似乎躍然紙上,而有些畫作,即使它們看起來基本上是真實的,但也不夠突出。在我們觀看的一些作品中,本應代表現實世界中平行線的線條最終沒有確定一個一致的消失點。觀看繪畫的任何一個部分,都沒有明顯的錯誤,但整體效果略有缺陷。當藝術家確實設法運用完美的透視——而觀眾設法找到正確的觀看點——效果會非常逼真。
正如克蘭內爾和她的合著者所描述的那樣:
我們可以看到幾何大師阿爾布雷希特·丟勒想要的效果。如果您[從數學確定的有利位置]觀看《書房裡的聖哲羅姆》,您會看到這幅版畫呈現出驚人的真實感和深度。畫面中的葫蘆似乎懸在你的頭頂;你感覺你可以把手伸進桌子下面的空間;左邊的長凳邀請你過來坐下,把枕頭弄蓬鬆。
如果您想知道如何親自找到那些蓬鬆的枕頭,克蘭內爾的網站上有關於射影幾何和透視藝術的資訊。
