本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
當我告訴人們我是數學家時,我會得到很多不同的反應。 也許令人驚訝的是,我大多得到積極的回應。 其中許多是“加油,女孩”之類的。 有些人會說,“我是[其他某種職業],但我一直喜歡數學”,或者“我希望我修過更多數學課。” 我得到一些“哇,你一定很聰明”的評論,這有點像話題終結者。 但當然,有些人告訴我他們討厭或害怕數學。
這裡有一個坦白:有時數學也讓我感到害怕。 所以在萬聖節,我將告訴你們一些我發現很怪異的數學:更高階同倫群。
同倫是數學領域拓撲學中的一個基本概念,拓撲學是對形狀最基本的研究。 如果你可以將一個物體拖到另一個物體上而無需切割任何東西,那麼這兩個物體就是同倫的。 同倫是如此基本,以至於一個空間的第一個同倫群被稱為基本群。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。 透過購買訂閱,您將有助於確保未來能夠繼續講述關於塑造我們當今世界的發現和想法的具有影響力的故事。
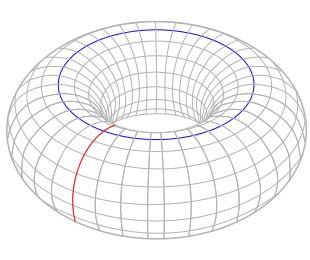
甜甜圈表面上以紅色和藍色突出顯示的兩條環線不是同倫的。 圖片:YassineMrabet,透過 Wikimedia Commons。 CC BY-SA 3.0
基本群,或 π1,與環線的同倫有關。 我將環線想象成無限彈性的橡皮筋。 你可以做任何保持橡皮筋完整並將其留在你正在研究的表面或空間上的事情。 如果你在籃球上放兩條橡皮筋,你總是可以拖動其中一條,使其與另一條對齊。 但是,如果你將一條橡皮筋繞在甜甜圈的孔上,另一條橡皮筋以另一種方式繞在孔上,你就無法將其中一條變形為另一條,而不會撕裂其中一條或離開甜甜圈的表面。 這告訴我們籃球和甜甜圈是不一樣的:它們沒有相同的第一個同倫群。 (以前絕對沒有辦法區分籃球和甜甜圈,所以我們有了拓撲學真是太好了。)
有一個關於拓撲學家的葷段子,它與“拓撲學家是無法區分結婚戒指和地上的洞,但可以區分它和地上的兩個洞的人”是同倫的。 (如果你知道這個笑話,那麼我的版本可能讓它看起來更葷。)這個笑話是關於基本群的,它基本上告訴我們一個物體有多少個洞。
基本群一開始很難理解。 但是,如果你坐下來想象一下表面上的橡皮筋一段時間,π1 就會開始變得有意義。 然後你學習關於 同調 群。 它們有點像第一個同倫群,因為它們也測量孔洞。 有時這些孔洞是更高維度的,因此更難以視覺化,但從道義上講,它們仍然是關於孔洞的。 例如,球體沒有一維孔洞——可以滑動圓圈的地方——但它有一個二維“孔洞”。 這有點讓人費解,但再一次,勇敢的拓撲學學生可以適應它們。
第一個同調群透過稱為 阿貝爾化 的東西與第一個同倫群相關。 阿貝爾化是什麼並不太重要,但它意味著第一個同調群比第一個同倫群稍微簡單一些。 這也意味著,至少對於你在基本拓撲學課程中看到的空間型別而言,第一個同倫群的描述並不比第一個同調群複雜多少。
第一個同調群和第一個同倫群之間的這種對應關係可能會讓毫無戒心的拓撲學學生產生一種虛假的安全感。 因為她聽說過被稱為“更高階同倫群”的東西,並假設它們一定與更高階同調群有類似的關係。 更高階同調群還不錯,所以更高階同倫群也不應該那麼糟糕。

前方有龍。 圖片:Friedrich Johann Justin Bertuch,透過 Wikimedia Commons。 PD-Art。
空間的第 n 個同倫群,稱為 πn,與從 n 維球體到空間的同倫不同對映的數量有關。 (對於我們的目的,圓圈是一維球體,籃球是二維球體,依此類推。)
n 維球體是最簡單的 n 維流形,因此 n 維球體的更高階同倫群應該是理解一般更高階同倫群的一個良好起點。 (她說道,幸福地沒有意識到自己的危險。)讓我們從 S2,二維球體開始。 我們已經看到 π1(S2) 是平凡的:球體上的任何環線都可以變形為任何其他環線,因此球體上只有一類環線。 為了計算 S2 的 π2,我們必須考慮我們可以用多少種不同的方式將球體“包裹”在自身周圍。 如果你想象在籃球周圍放一個非常有彈性的袋子,你可以將其包裹一次,或者你可以將其包裹兩次、三次或任意整數次。 會有一些奇怪的地方袋子會被擠在一起,但你可以想象,一旦你將袋子包裹了幾次並將其密封起來(這需要袋子自身交叉;這對我們來說不是問題),你將袋子包裹在籃球周圍的次數將告訴你一些關於你擁有的地圖型別的資訊。 因此,S2 的第二個同倫群由整陣列成。

球體上的一些點及其在霍普夫纖維化中的纖維的視覺化。 圖片:Niles Johnson,透過 Wikimedia Commons。 CC BY-SA 3.0。
那麼 S2 的 π3 呢? 這是我的直覺失敗的地方。 對於同調群,二維流形不可能有任何三維孔洞,因此對於 S2 來說,第三個同調群及以上的所有同調群都是平凡的。 我希望同倫群也是如此。 但是在 1931 年,海因茨·霍普夫發現了霍普夫纖維化,這是一個從 3 球體到 2 球體的連續函式,它與恆等對映不同倫。 因此,S2 的 π3 並不像我認為的那樣平凡,而是實際上由 霍普夫纖維化 生成。
S2 的其餘更高階同倫群變得更加奇怪。 π6(S2) 是一個具有 12 個元素的迴圈群,這意味著存在一些從 S6 到 S2 的對映,其中執行 12 次會將你帶回到與恆等同倫的東西。 π14(S2) 由一個 84 階對映和兩個 2 階對映生成。 我起了雞皮疙瘩,而我們才剛剛開始研究 S2!
球體的同倫群中有很多怪異的模式,所以如果你敢的話,你應該 檢視它們。 我受不了鬼屋,所以我就在這裡玩我的無限彈性橡皮筋。
