本文發表於《大眾科學》的前部落格網路,僅反映作者的觀點,不一定代表《大眾科學》的觀點。
在本期《我最喜歡的定理》節目中,我的聯合主持人凱文·克努森和我很榮幸採訪了亨利·福勒。福勒博士是Diné學院數學系主任,該學院為納瓦霍民族服務。您可以在kpknudson.com收聽節目。
我在十月份的SACNAS(科學促進奇卡諾人和美國原住民協會)年度會議上見到了福勒博士。對我來說很方便的是,會議地點離我在鹽湖城的家很近,騎腳踏車即可到達。福勒博士在會議上就他為改善納瓦霍社群的數學教育所做的努力發表了感人的主題演講。他參與的主要專案之一是數學圈,這是一種為初中和高中學生及其教師提供的數學強化專案。這可能會讓一些播客聽眾和部落格讀者想起一些事情,因為喬治·西瑟裡最近製作了一部關於這項工作的紀錄片,名為《納瓦霍數學圈》。
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道: 訂閱。透過購買訂閱,您將有助於確保未來能夠繼續釋出關於塑造我們當今世界的發現和思想的有影響力的報道。
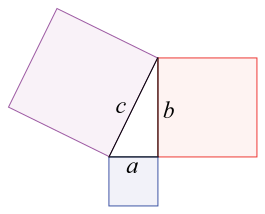
勾股定理指出,在這個邊長分別為a、b和c的直角三角形中,這些邊長滿足關係式a2+b2=c2。在圖中,藍色和紅色正方形放在一起的面積與紫色正方形的面積相同。圖片來源:Wapcaplet Wikimedia(CC BY-SA 3.0)
對於他最喜歡的定理,福勒博士選擇了勾股定理,這可能是數學中最著名的定理。該定理斷言直角三角形的兩條直角邊a和b與斜邊c之間的關係:a2+b2=c2。雖然現在大多數人透過希臘數學家畢達哥拉斯的名字知道它,但在畢達哥拉斯出生之前很久,包括北美在內的許多地方的人們就已經知道這些長度之間的關係。福勒博士談到了納瓦霍人傳統上使用勾股定理的許多方面,包括距離計算、天文觀測和建築施工。
在播客的每一集中,我們都會請嘉賓將他們最喜歡的定理與某物配對:食物、飲料、藝術、音樂或生活中其他非數學的樂趣。福勒博士的定理配對有點不尋常。他談到了勾股定理如何與他作為納瓦霍人的傳統產生交集,包括他的成長經歷如何在某些方面幫助他發現自己在數學方面的天賦和興趣。
您可以透過在本月(2017年11月;該連結可能在本月之後仍然可用)在PBS上觀看紀錄片來了解更多關於納瓦霍數學圈的資訊。您還可以在Zala Films網站上找到有關該紀錄片的資訊。
您可以在 kpknudson.com 和 Roots of Unity上找到更多關於本播客中介紹的數學家和定理的資訊,以及其他令人愉悅的數學趣味內容。文字稿可在此處獲取。您可以在iTunes和其他播客分發系統上訂閱和評論播客。我們很樂意聽取聽眾的意見,請傳送郵件至myfavoritetheorem@gmail.com與我們聯絡。凱文·克努森的Twitter賬號是 @niveknosdunk,我的賬號是 @evelynjlamb。節目本身也有一個Twitter feed: @myfavethm 和一個 Facebook頁面。請在下次加入我們,學習另一個引人入勝的數學知識。
《我最喜歡的定理》往期回顧
第0集:主持人最喜歡的定理 第1集:艾米·威爾金森最喜歡的定理 第2集:戴夫·裡奇森最喜歡的定理 第3集:埃米爾·戴維·勞倫斯最喜歡的定理 第4集:喬丹·艾倫伯格最喜歡的定理 第5集:杜薩·麥克達夫最喜歡的定理 第6集:惠理子·廣中(Eriko Hironaka)最喜歡的定理
