在野外遭遇組合數學

本文發表於《大眾科學》的前部落格網路，反映了作者的觀點，不一定反映《大眾科學》的觀點

我最近搬家了，新家比舊家離合唱團練習的地方稍遠。我走去那裡的路程變長了，給了我更多的時間在漫步時沉浸在思考中。有什麼比思考步行本身更好的主題呢？具體來說，作為一名數學家，我想找到我家和合唱團練習地點之間的最佳路線。

我的舊家幾乎在合唱團練習地點的正北方，所以步行到那裡沒有太多選擇。但是，新家在北方八個街區和西方六個街區。街道呈網格狀，因此任何向南走八個街區，向東走六個街區的路線都可以到達合唱團練習地點。

關於支援科學新聞

如果您喜歡這篇文章，請考慮透過以下方式支援我們屢獲殊榮的新聞事業 訂閱。透過購買訂閱，您正在幫助確保未來能夠繼續講述關於塑造我們今天世界的發現和想法的具有影響力的故事。

這些路線基本上長度相同，所以我不是要儘量縮短距離。相反，我只是想找到最令人愉快的通勤方式：即遇到最少咆哮的狗，有最佳的繁忙街道交叉口，以及最美麗的風景可以在路過時欣賞。我不知道有什麼捷徑可以找出我的最佳通勤路線，所以我只需要嘗試所有可能性。我不希望在我的路線上折返，所以我想弄清楚有多少種方法可以只向南和向東走 8 個街區向南和 6 個街區向東。

我對組合數學略知一二，組合數學是數學的一個分支，處理計算牌組、椅子上的學生，或者在我的情況下是去合唱團練習的路徑的組合和排列，但我不是專家。然而，當我在最近的一次散步中思考這個問題時，我意識到它令人難忘地熟悉。事實上，幾個月前我剛剛在 Project Euler 上解決了這個問題。Project Euler 是一個很棒的數學問題資料庫，需要一些程式設計來解決。我還是程式設計新手，Project Euler 是我獲得有趣的問題來練習和練習我的 Sage 技能的好地方。

問題 15，“網格路徑”，要求我們找到在 20x20 網格中僅向下和向右移動，從左上角到右下角的不同路線的數量。

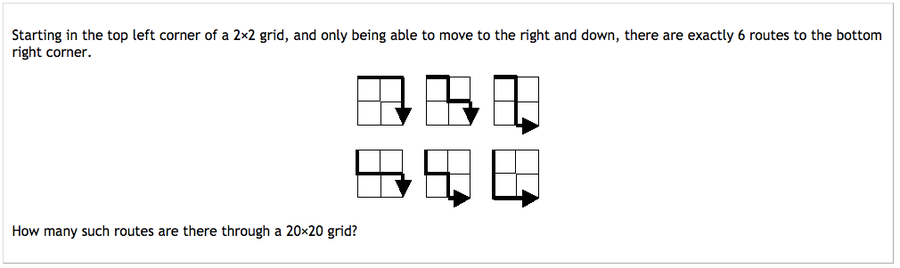
數字略有不同，但這正是我想要解決的問題，以弄清楚有多少種可能的路線可以到達合唱團練習地點。

那麼答案是什麼呢？好吧，Project Euler 的第一條規則是不要談論 Project Euler。或者至少不要談論你是如何解決 Project Euler 問題的。正如主頁所說，“真正的學習是一個積極的過程，看到它是如何完成的與體驗發現的頓悟相去甚遠。請不要剝奪他人您自己如此珍視的東西。”

因此，我不會告訴您有多少條路徑，也不會告訴您我是如何計算出來的。（如果您計算出來，請不要破壞其他人的樂趣。）但是，我要說的是，我和我的數學家配偶提出了一個詳盡的解決方案，但最終遠非解決此問題的最快方法。雖然當我看到更簡潔的答案並意識到事後看來它是多麼明顯時，我感到有點傻，但我們的方法揭示了組合數學中一個新的（對我而言）恆等式。我對此真的不會生氣。

我用來解決 Project Euler 問題的方法完全適用於市中心步行的情況，因此我現在知道在對哪條路線是最佳路線做出判斷之前，我需要嘗試多少條路線。讓我們只說我有足夠的

work步行任務要完成。