本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
在本期《我最喜歡的定理》節目中,凱文·克努森和我很榮幸與艾米莉·戴維·勞倫斯交談。她是舊金山大學的數學教授,研究低維拓撲學。你可以在這裡或在kpknudson.com收聽,那裡也有本期節目的文字稿。
對於她最喜歡的定理,勞倫斯博士選擇了緊曲面分類,這是拓撲學入門課程中最棒的定理之一。分類定理指出,所有滿足一些溫和要求的曲面都拓撲等價於球面、環面之和或射影平面之和。(碰巧的是,我之前寫過關於環面的文章,一篇關於射影平面的文章也即將釋出。這是一種令人愉悅的不可定向曲面,就像更強烈的莫比烏斯帶。)拓撲等價允許很大的自由度。只要你可以將一個形狀變形為另一個形狀,而無需刺穿或粘合任何東西,這兩個形狀就是拓撲等價的。
關於支援科學新聞業
如果您喜歡這篇文章,請考慮透過 訂閱。透過購買訂閱,您正在幫助確保未來能夠繼續講述關於塑造我們當今世界的發現和思想的有影響力的故事。
緊曲面分類定理指出,就拓撲學而言,環面和射影平面構成除球面以外的所有其他曲面的構建塊,球面只是孤立存在。如果您想知道取兩個曲面的和是什麼意思,這非常直觀。你只需在每個曲面上切一個小孔,然後沿著孔將兩個曲面縫合在一起。

兩個曲面連通和過程的圖示。鳴謝:Oleg Alexandrov Wikimedia (CC BY-SA 3.0)
如果你聽過《我最喜歡的定理》第 0 集,勞倫斯博士最喜歡的定理聽起來可能很熟悉。它與我個人最喜歡的定理,一致化定理密切相關。它們適用於略有不同的曲面型別。曲面分類定理適用於任何沒有任何穿孔的二維曲面,而一致化定理僅適用於稱為黎曼曲面的曲面。最重要的區別在於黎曼曲面必須是可定向的,因此一致化定理不適用於射影平面之和,而曲面分類定理對此沒有問題。一致化定理不是按拓撲結構對曲面進行分類,而是說可定向曲面可以有三種不同的幾何型別。它可以與曲面分類定理結合,表明每個可定向曲面都有一個自然的幾何結構。像沙灘球這樣沒有孔洞的曲面,自然具有球面或橢圓幾何。有一個孔洞的曲面自然具有平面幾何,而有多個孔洞的曲面自然具有雙曲幾何。
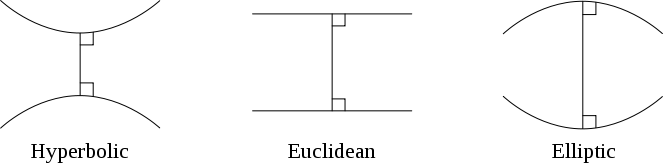
雙曲幾何、歐幾里得幾何和橢圓(或球面)幾何的圖示。在雙曲幾何中,平行線彼此遠離。在歐幾里得幾何中,它們保持相同的距離。在橢圓幾何中,沒有不相交的線。鳴謝: Pbroks13 和 Joshuabowman Wikimedia (CC BY-SA 3.0)
勞倫斯博士決定用一個經典的配對來解釋她的定理:甜甜圈和一杯咖啡。這指的是一個經典的數學笑話:拓撲學家是那種無法區分甜甜圈和一杯咖啡的人,因為當您拉伸或擠壓表面時,它們是等價的,兩者都有一個孔。

馬克杯和甜甜圈拓撲等價性的演示。鳴謝:Lucas V. Barbosa Wikimedia
您可以在kpknudson.com和Roots of Unity找到更多關於本播客中介紹的數學家和定理的資訊,以及其他令人愉悅的數學趣味內容。文字稿在此處可用。您可以在 iTunes 和其他播客分發系統上訂閱和評論播客。我們很樂意聽到聽眾的來信,所以請傳送郵件至 myfavoritetheorem@gmail.com。凱文·克努森的 Twitter 賬號是 @niveknosdunk,我的賬號是 @evelynjlamb。該節目本身也有一個 Twitter 賬號:@myfavethm 和一個 Facebook 頁面。下次加入我們,學習另一個引人入勝的數學知識。
《我最喜歡的定理》節目回顧
