本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點。
本月早些時候釋出的 Numberphile影片 聲稱所有正整數的和為 -1/12。
我通常是 Numberphile 團隊的粉絲,他們出色地使數學變得令人興奮和易於理解,但這個影片讓我感到失望。將數字 -1/12 與級數 1+2+3+4... 聯絡起來是有意義的方法,但在我看來,稱其為級數的和是具有誤導性的。此外,它的呈現方式助長了我作為數學教育者經常遇到的一個誤解,即數學家們在毫無明顯理由的情況下武斷地改變規則,學生們對在特定情況下什麼是允許的,什麼是不允許的,沒有任何希望瞭解。在關於這個影片的一篇文章中,物理學家 Dr. Skyskull 說,“令人沮喪的是,很大一部分人自動認為數學是一些非直觀的、奇異的巫術,只有超級智慧的人才能理解。在沒有任何限定的情況下展示這樣一個瘋狂的結果只會加強這種觀點,而且在我看來,這對數學是一種損害。”
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道: 訂閱。透過購買訂閱,您正在幫助確保關於塑造我們今天世界的發現和想法的有影響力的故事的未來。
加法是一種二元運算。你輸入兩個數字,然後得到一個數字。但你可以將其擴充套件到更多數字。例如,如果您有三個數字要相加,您可以先將其中任意兩個數字相加,然後將第三個數字加到結果和中。我們可以對任意有限數量的加數重複此操作(算術定律表明,無論我們以什麼順序相加,我們都會得到相同的答案),但是當我們嘗試將無限數量的項相加時,我們必須選擇加法的含義。處理無限加法最常見的方法是使用極限的概念。
粗略地說,我們說如果當我們新增越來越多的項時,我們越來越接近數字 L,那麼無窮級數的和就是一個數字 L。如果 L 是有限的,我們稱該級數為收斂級數。收斂級數的一個例子是 1/2+1/4+1/8+1/16…。這個級數收斂於數字 1。很容易看出原因:在第一項之後,我們離 1 還差一半。在第二項之後,我們離 1 還差剩餘距離的一半,依此類推。
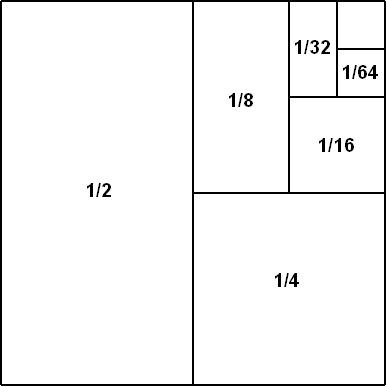
1/2+1/4+1/8...=1 的視覺化“證明”。圖片來源:Hyacinth,透過 Wikimedia Commons。
芝諾悖論 說我們永遠不會真正達到 1,但從極限的角度來看,我們可以儘可能接近我們想要的。這就是數學家在談論無窮級數時通常所說的“和”的定義,它基本上符合我們對“和”和“等於”這兩個詞的直觀定義。
但並非每個級數在這種意義上都是收斂的(我們將非收斂級數稱為發散級數)。有些級數,如 1-1+1-1…,可能會在我們不斷新增更多項時在不同的值之間跳動,而有些級數,如 1+2+3+4...,可能會變得任意大。很明顯,那麼,使用級數收斂的極限定義,級數 1+2+3… 不收斂。如果我說,“我認為這個級數的極限是某個有限數 L,”我可以很容易地計算出要加多少項才能達到我想要的數字 L 以上的程度。
將數字 -1/12 與級數 1+2+3... 聯絡起來是有意義的方法,但我更願意不將 -1/12 稱為正整數的“和”。解決這個問題的一種方法是使用複分析中的解析延拓的思想。
假設您有一個函式 f(z),它定義在複平面中的某個地方。我們將函式定義的域稱為 U。您可能會找到一種方法來構造另一個函式 F(z),該函式定義在更大的區域中,使得當 z 在 U 中時,f(z)=F(z)。因此,新函式 F(z) 在 f(z) 定義的任何地方都與原始函式 f(z) 一致,並且它在 f(z) 域外的一些點處定義。函式 F(z) 稱為 f(z) 的解析延拓。(“The”是合適的冠詞,因為函式的解析延拓是唯一的。)
解析延拓很有用,因為複函式通常定義為涉及變數 z 的無窮級數。然而,大多數無窮級數僅對 z 的某些值收斂,如果我們能讓函式在更多地方定義,那就太好了。函式的解析延拓可以為函式定義在其無窮級數定義收斂區域之外的值。我們可以透過將函式的解析延拓追溯應用到其原始無窮級數定義來說 1+2+3...=-1/12,這種做法應該伴隨著 Lucille Bluth 式的眨眼。

問題中的函式是黎曼 zeta 函式,它以其與關於素數分佈的問題的深刻聯絡而聞名。當 s 的實部大於 1 時,黎曼 zeta 函式 ζ(s) 定義為 Σ∞n=1n-s。(我們通常使用字母 z 作為複函式中的變數。在這種情況下,我們使用 s 是為了尊重黎曼,他在 1859 年的論文 [pdf] 中定義了 zeta 函式。)當 s=-1 時,這個無窮級數不收斂,但你可以看到,當我們代入 s=-1 時,我們得到 1+2+3…。黎曼 zeta 函式是此函式到整個複平面減去點 s=1 的解析延拓。當 s=-1 時,ζ(s)=-1/12。透過在 ζ(-1) 和在複平面的其他部分定義該函式的正式無窮級數之間放一個等號,我們得到 1+2+3...=-1/12 的陳述。

解析延拓不是將數字 -1/12 與級數 1+2+3... 聯絡起來的唯一方法。有關一種不需要複分析的方法的非常好的、深入的解釋(包括家庭作業練習),請檢視 Terry Tao 關於這個主題的帖子。
Numberphile 影片讓我感到困擾,因為他們有機會談論為無窮級數賦值的意義,並解釋不同的方法。如果您已經對該主題有所瞭解,您可以觀看該影片和關於該主題的更長的相關影片,並瞭解真正發生的事情的片段。但是,如果觀眾認為“和”的含義與他們認為的含義相同,那麼對於一堆正數加起來等於一個負數來說,影片的“哇”因素就來自於它毫無意義的事實。
.jpg?w=350)
透過 quickmeme。
如果 Numberphile 團隊更明確地說明將數字與級數關聯的替代方法,他們本可以做的不僅僅是讓人認為數學家總是在改變規則。在影片的結尾,製片人 Brady Haran 問物理學家 Tony Padilla,如果他在計算器上永遠新增整數,最後按下“等於”按鈕,是否會得到 -1/12。Padilla 厚顏無恥地說,“你必須達到無窮大,Brady!” 但答案應該是“不!” 在這裡,我認為他們錯過了一個機會來澄清他們正在使用一種為無窮級數賦值的替代方法,這將使影片的誤導性大大降低。
其他人已經寫了一些關於這個影片中數學的好東西。在 Slate 部落格文章 對此過度輕信之後,Phil Plait 寫了一篇更加冷靜的解釋,解釋了為級數賦值的不同方法。如果您想自己研究“證明”的細節,John Baez 已經為您準備好了。Blake Stacey 和 Dr. Skyskull 寫了關於用數字 -1/12 代替正整數的和在物理學中如何有用的文章。Richard Elwes 釋出了一個無窮級數“健康和安全警告”,其中涉及我最喜歡的調和級數。我認為關於這個無窮級數意味著什麼的大量討論是好的,即使我希望更多的討論可以在影片中進行,到目前為止,該影片在 YouTube 上的觀看次數已超過一百萬次!