本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點。
幾年前,當弗蘭克·法里斯在聯合數學會議上談論他的藝術展覽 《看見對稱》時,我第一次聽說他的作品,並立刻被迷住了。不久之後,我讀到了他的“不可能的桌布”,它似乎具有數學上不可能的五重旋轉對稱性。現在他出版了一本關於他作品的書,《創造對稱:桌布圖案的巧妙數學》。這本書是一本精美的圖文指南,旨在融合數學和藝術創造力,以生成引人入勝且視覺上吸引人的設計。
《創造對稱》涵蓋了與對稱性相關的數學的幾個不同方面。 廣義上講,法里斯從曲線的對稱性開始,轉移到歐幾里得平面中的對稱性,最後探索球面幾何和雙曲幾何中類似的對稱性。 在數學上,本書結合了複分析、傅立葉級數、抽象代數和現代幾何。 雖然這個列表看起來令人生畏,但沒有任何先決條件。 這些解釋是獨立的且清晰的。
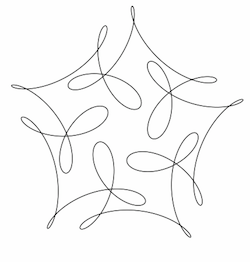
弗蘭克·法里斯的“神秘曲線”。 公式為 µ(t)=(cos(t)+cos(6t)/2+sin(14t)/3, sin(t)+sin(6t)/2+cos(14t)/3)。 五重對稱性從何而來? 圖片:弗蘭克·法里斯,©普林斯頓大學出版社。經許可使用。
關於支援科學新聞業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞業 訂閱。 透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
第一章向我們介紹了一條誘人的“神秘曲線”。 神秘之處不在於曲線的公式,而在於它為什麼看起來是這個樣子。 該函式是正弦和餘弦的組合,其中有很多 6 和 14 在浮動,但不知何故它具有五重旋轉對稱性。 “花點時間用你的眼睛追蹤它,欣賞它舞動的起伏,”法里斯寫道。 “我希望這個圖形——‘神秘曲線’——會讓你感到驚訝。” 這條曲線提供了深入研究三角函式組合中的係數如何影響結果曲線外觀的動力。 (有關此類曲線的更多資訊,包括互動式曲線生成器,請參閱 Mike Croucher 的帖子,靈感來自法里斯和 John D. Cook。)
正如神秘曲線的情況一樣,視覺化貫穿本書始終推動著數學的發展。 在一章中,法里斯寫道,
在研究桌布函式多年後,當我以為至少從數學的角度來看,這個故事不可能再新增任何東西時,我的螢幕上出現了一張影像。 我稱之為“快樂的意外時刻”,因為隨機選擇的桌布係數導致了一些我認為可以構成一個相當好的故事的東西。
像這樣的“快樂的意外”在書中多次出現,它們幫助讀者理解對於法里斯來說,數學和藝術的創造力如何相互促進。
本書的大部分內容致力於桌布群和飾帶群。 桌布群描述了在平面中兩個方向上具有對稱性的圖案,而飾帶群描述了在一個方向上具有對稱性的圖案。 這些群組是很有吸引力的主題,有很多方法可以瞭解它們,從代數教科書到 YouTube 影片。
.jpg?w=300)
山峰上的桃子及其負片為帖子頂部的變形飾帶和下方的雙曲桌布建立了“色輪”。 圖片:弗蘭克·法里斯,©普林斯頓大學出版社。經許可使用。
對我來說,《創造對稱》與眾不同之處主要有兩點。 首先是如何無縫地將幾何和代數結合起來描述這些圖案。 第二是顏色。 視覺化平面的變換可能很困難,因為這種變換的“圖表”將存在於四維空間中。 解決這個問題的一種常見方法是以某種方式為平面著色,並顯示變換“之前”和“之後”的圖片。 (有關此方法的美麗示例,請參閱關於莫比烏斯變換的這段影片。)法里斯接受了這個想法並加以應用。 法里斯沒有使用簡單的色輪或正方形網格,而是使用了他自己的照片,或者正如他所描述的那樣,“世界是我的色輪”。
.jpg?w=300)
由上面的 Kaiser Peach 色輪製成的雙曲桌布圖案。 圖片:弗蘭克·法里斯,©普林斯頓大學出版社。經許可使用。
法里斯為函式著色的方法使數學和藝術之間的競爭環境趨於平等。 法里斯不僅僅使用顏色來說明數學函式,他還使用數學將風景、花卉或晚餐的快照轉化為美麗的設計。 數學和設計是平等的夥伴。 法里斯多次使用一些相同的色輪,看到從一個來源可以湧現出多少不同的圖案,這真是令人著迷。 我最喜歡的色輪是Kaiser Peach,如上圖所示,部分原因是它的故事。 法里斯寫道:“攀登內華達山脈的凱撒峰是一個受歡迎的朝聖之旅,帶一個桃子到山頂是一種使桃子味道特別美妙的傳統方式。”
法里斯的色輪激發了他超越 17 個桌布群和 7 個飾帶群。 透過建立由影像及其負片組成的色輪,旋轉 180 度,他引入了顏色反轉對稱性。 顧名思義,在這些對稱性中,影像的變換最終使形狀保持不變,顏色切換為其負片。 透過使用顏色的“旋轉”而不是負片,他將這個想法進一步推廣到“顏色旋轉”對稱性,例如,平面的三重旋轉將橙色變為紫色,紫色變為綠色,綠色變為橙色。
《創造對稱》是為誰而寫的? 這本書不是典型的流行數學讀物。 它包含大量的方程式和技術細節,我可以看到它在幾種不同的情況下可以作為教科書發揮作用:作為複分析或抽象代數的補充,或者作為不尋常的本科數學選修課的組織框架,可以更深入地研究每個主題。 但是,儘管這本書可以作為教科書,但它仍然溫暖而友好,沒有高等數學背景的人也可以欣賞它,只要他們不介意跳過一些明確標記的技術部分。 法里斯的善良、熱情和略帶古怪的幽默感(例如,他透露他會暫停電影來檢查背景中桌布的對稱群)使原本可能枯燥的主題變得引人入勝。 到最後,您可能已準備好為自己創造對稱性。
