本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
海豚的三角剖分。圖片來源:Crhschn,透過維基共享資源。
曲面是複雜的。三角形是簡單的。這是建立計算機圖形和一些高等數學背後的一種思想。如果我們有一個曲面,我們可以取曲面上的一堆點,並將它們連線成三角形,以獲得曲面的近似值。這很好,但是三角剖分有多可靠?它在多大程度上反映了原始曲面的屬性?例如,當我們增加曲面近似值中三角形的數量時,三角剖分曲面的表面積會接近原始曲面的表面積嗎?

卡爾·赫爾曼·阿曼杜斯·施瓦茨,他是第一個描述施瓦茨燈籠的人。圖片來源:公共領域,透過維基共享資源。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關當今塑造我們世界的發現和想法的具有影響力的故事的未來。
1880年,數學家和正義的鬍鬚維護者赫爾曼·施瓦茨透過產生一個反例,一個曲面和一系列三角剖分近似值,否定地回答了這個問題,對於這些近似值,三角剖分的表面積變得任意大,因此不收斂到原始曲面的表面積。
本學期早些時候,我有機會參加當地女性數學協會分會舉辦的摺紙工作坊。拉迪卡·古普塔是猶他大學的研究生,她向我們展示瞭如何僅透過摺疊紙張來製作這個被稱為施瓦茨燈籠的反例。
要製作施瓦茨燈籠,我們從一張紙開始。
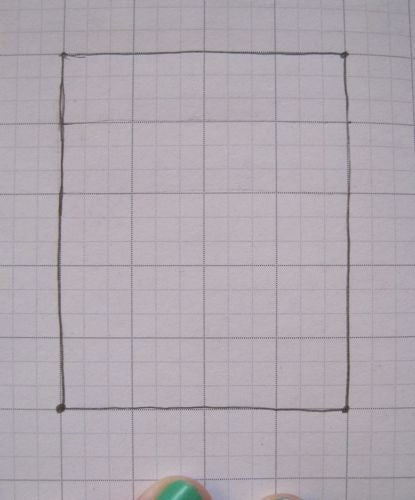
圖片來源:伊芙琳·蘭姆。
我們將紙張的長度分成 M 部分,這樣我們就得到了 M 個細長的水平矩形。
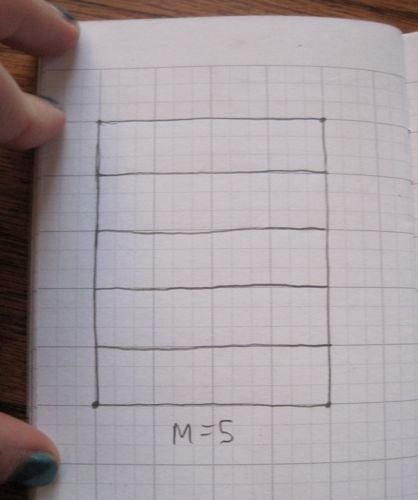
圖片來源:伊芙琳·蘭姆。
然後,每個細長的水平矩形透過在頂部和底部以偏移量放置 N 個點並將這些點連線成三角形,從而分成 2N 個三角形。(請注意,最後,左右兩側將粘合在一起,因此繪製了一些三角形,以便在粘合前一半在右側,一半在左側。)
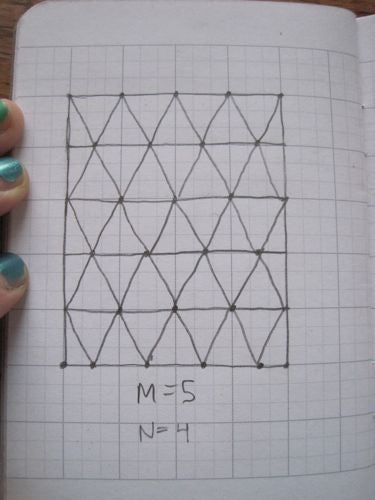
圖片來源:伊芙琳·蘭姆。
現在我們只需要將水平線“向內”摺疊,將對角線“向外”摺疊,並將右側貼上到左側,以獲得一個由三角形面組成但看起來有點像圓柱體的表面。(注意:此步驟有點困難。我不得不向工作坊負責人古普塔和我的一個學生尋求幫助,他是一位才華橫溢的摺紙愛好者。您可能也需要幫助。)

我和我的朋友們一起製作的施瓦茨燈籠。頂點(尖點)都位於圓柱體上。(這不是用前三張圖片中的紙張製作的。它比那張紙張有更多的三角形。)圖片來源:伊芙琳·蘭姆。
隨著 M 和 N 的增加,三角剖分在某種意義上收斂到圓柱體:隨著三角形數量的增加,三角剖分上任何點與圓柱體上點之間的距離趨於 0。但是,根據 N 與 M 的比率,三角剖分的表面積可能不會收斂到圓柱體的表面積。如果 N 比 M 大得多(特別是,如果比率 N/M 不趨於 0),則三角剖分的表面積會變得任意大。另一種思考方式是,如果 N 相對於 M 非常大,那麼隨著 N 和 M 的增加,當您將它們摺疊起來時,得到的圓柱體就會越來越小。
值得問一下,我們是否應該對能夠建立這個反例感到驚訝。我們應該期望曲面的三角剖分近似值具有與曲面本身相同的屬性嗎?當我在嘗試決定施瓦茨燈籠是令人震驚還是僅僅有趣時,我想到了當我們提出關於平面曲線的類似問題時會發生什麼。當我們用多邊形(具有直邊的形狀)近似平面中的彎曲形狀時,多邊形的周長會收斂到彎曲形狀的周長嗎?不一定。讓我們只考慮一個圓作為我們要近似的形狀。如果我們限制我們的近似值為正凸多邊形(您的標準等邊三角形、正方形等),那麼我們可以透過增加正多邊形的邊數來近似圓。在這種情況下,隨著邊數的增加,多邊形的周長確實會趨於圓的周長。但是,如果我們放寬規則,則可以繪製一系列看起來收斂到圓但其周長始終頑固地等於 4 的多邊形。有關該構造的精彩解釋,請參閱 Vi Hart 的影片π=4 的證明狂想曲。雖然這不是一個完美的類比,但我認為施瓦茨燈籠的想法與該影片中的想法相似,因此在某種意義上,它的存在並不太令人驚訝。
有關施瓦茨燈籠的更多資訊,請檢視Conan Wu 的部落格文章或其在Cut the Knot上的頁面。Wu 的帖子包括一個可列印的模板和製作您自己的說明!

從上方看到的施瓦茨燈籠。圖片來源:伊芙琳·蘭姆。