本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定代表《大眾科學》的觀點
2003 年,當我還是大學二年級學生時,我很高興地越來越深入地研究音樂理論和數學。為了配合我的個人風格,我為 20 世紀音樂課的作業寫了一個 12 音序列,以表達微積分基本定理的一個陳述。
正如 Vi Hart 在下面的精彩影片中所解釋的那樣,12 音序列主義是在 20 世紀初提出的,目的是鼓勵作曲家擺脫傳統的調性,創作出沒有任何音符比其他音符更重要的音樂。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保有關當今世界發現和塑造我們世界的具有影響力的故事的未來。
序列作曲家從一個音列開始,該音列是八度音階中十二個半音(或 12 個鋼琴琴鍵:C-C#-D-D#-E-F-F#-G-G#-A-A#)的排序。
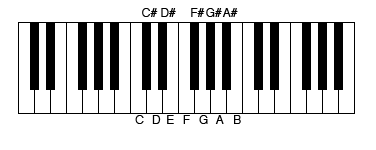
一個鍵盤草圖,顯示構成 12 音音列中音符的 12 個音高。來源:Evelyn Lamb,基於Spindoktoren Wikimedia (CC BY-SA 3.0)
我在我的作品中使用的音列是 F#-A-E-D-C#-F-B-G-G#-A#-D#-C。

我的音列,記在五線譜上。來源:Evelyn Lamb
該音列及其某些修改形式,例如將音列移調到不同的音符開始或倒退演奏,提供了作品中允許的材料。作曲家必須按照順序使用這些音列中的音高(在任何八度音階中),然後再重複使用較早的音高。(一些作曲家對規則的解釋略有不同,但這就是要點。)這是我的歌曲中人聲部分的第一行。
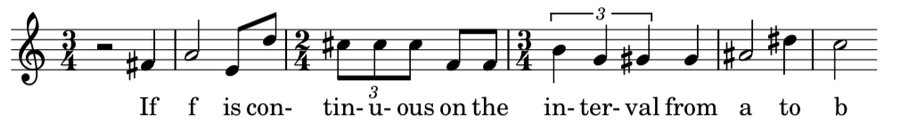
來源:Evelyn Lamb
我的作品絕非天才之作(要聆聽 12 音序列天才之作,請檢視 Alban Berg 的抒情組曲),但如果我這麼說,我的音列還是很棒的。開頭和結尾的四音組讓人想起傳統的調性,但整個音列足夠崎嶇,足以讓事情變得有趣。但我特別自豪於音列的另一個特點:就像《抒情組曲》中的主要音列之一一樣,它包含 12 音系統中兩個音符之間所有可能的音程。(邏輯上來說,這樣的音列被稱為全音程音列。)
如果您還不熟悉音樂音程的名稱,這沒什麼大不了的。如果您可以想象在鋼琴上彈奏音符,您可以計算鋼琴琴鍵,以半音為單位告訴您音程。我的音列中的第一個音程 F#-A,是一個升小三度或一個降大六度,這取決於作曲家選擇 A 比 F# 高還是低。為了實用起見,我將始終參考音程升序版本的半音數,因此 F#-A 是 3 個半音的音程。音列中的下一個音程 A-E 是一個升純五度,7 個半音。音程 E-D 是 10 個半音,依此類推。我的音列中完整的音程式列是 3-7-10-11-8-6-1-2-5-9。兩個連續音高之間的每個音程都不同,這意味著從 1 到 11 的每個可能音程都出現在其中某個位置。
我為找到這個全音程音列感到自豪,這一發現讓我想找到更多的全音程音列並弄清楚如何描述它們。最終,我開始注意到我找到的音列中的一些常數:三全音(6 個半音的音程,在我的音列中,在 F 和 B 之間)總是正好在中間,並且音程具有很好的對稱性。第一個音程是 12 減去最後一個音程,第二個音程是 12 減去倒數第二個音程,依此類推。考慮此屬性的另一種方法是,倒退演奏的音列與原始版本的音列具有相同的音程。
注意到這些模式後,我開始嘗試從數學上證明每個全音程音列都必須具有相同的屬性。我一直被卡住。誠然,我當時在數學上並不特別精通。我剛剛開始上一門證明入門課,我的數學技能更多的是計算而不是理論。但我缺乏精通,我用時間來彌補。我花了很多時間在這個問題上,但毫無進展。最終我繼續我的生活,但這個問題一直困擾著我。多年來,每當我有紙並且非常不想做當時我應該做的事情時,我都會時不時地回到這個問題上。仍然一無所獲。
最終,幾年前,我決定放棄並看看是否有人為我證明了這個定理。令我震驚的是,我發現這個問題在 1965 年就已被研究過,我錯了!(我忘記了嘗試證明定理的關鍵部分:你應該花一部分時間嘗試反駁它!)在《新音樂的視角》一篇名為“關於十一音程十二音列”的論文中,Stefan Bauer-Mengelberg 和 Melvin Ferentz 詳細描述了他們透過計算機輔助列舉全音程音列的路徑。
這篇論文有一些可愛的小細節。在腳註中,作者描述了一些熟悉的感受
透過消除以外的程式獲得音程音列的問題已被證明具有高度傳染性,在整個 1963 年,作者和他們的許多同事一直在相互再感染。在他們發燒的狀態下,他們提出了許多假設,但大多數都被證明是錯誤的……
得知他們的兩個假設與我的假設相同,我感到很欣慰:一個全音程音列在正向或反向閱讀時具有相同的音程,並且三全音將在中間。(他們寫了前一個猜想,“支援它的有力證據是 [作曲家和音樂理論家] Milton Babbitt 無法立即提出反例。”)但研究這個問題的 IBM 研究人員給了他們兩個反例
C-B-D#-F-G#-C#-G-E-D-A-A#-F#

一個反例音列。來源:Evelyn Lamb
C-D#-E-A-B-A#-G#-F-C#-G-D-F#

第二個反例,粉碎了我所有的偉大夢想。來源:Evelyn Lamb
在第一個反例中,三全音(C# 和 G 之間)在音列的中間;在第二個反例中,三全音(也在 C# 和 G 之間)是倒數第三個音程。
Bauer-Mengelberg 和 Ferentz 將音樂條件轉化為關於排列的數學問題,並編寫了一個計算機程式來查詢可以生成全音程音列的所有排列。在 IBM 7094 上執行七分十二秒後,有 1,928 個這樣的排列,每個排列都可以用來建立 24 個不同的全音程音列,總共有 46,272 個全音程音列,而在 479,001,600 個可能的音列中,大約是 1/10,000(巧合的是,與一個有 14 個孩子的家庭全部生男孩的機率相似)。
Bauer-Mengelberg 和 Ferentz 希望找到簡單的數學條件,使其能夠找到並描述所有全音程音列。相反,在進行一些基本的簡化之後,他們找到音列的方法歸結為蠻力,列出可能的排列並剔除不具有所需屬性的排列。這種缺乏結果讓他們感到值得注意。他們寫道:“事實上,迄今為止獲得的最有趣的結果也許是,這些結構的數學特徵,正如我們將看到的那樣,非常簡單,但在某些方面卻如此難以分析。”我很高興不僅是我一個人!
後來的研究,包括 Robert Morris 和 Daniel Starr 的“全音程系列的結構”,提供了一些分類和生成全音程音列的替代方法,但它們仍然有些神秘。沒有容易讓人類執行的生成它們的配方,並且它們並非都具有相同的屬性。我很欣慰,我終於在我對全音程音列進行數學描述的探索中找到了答案,即使這是因為我錯了。
