本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
歐幾里得幾何,大約在公元前300年由亞歷山大的歐幾里得在歷史上最具影響力的教科書之一中編纂而成,它基於23個定義、5個公設和5個公理,或“公認概念”。但正如我在我最近關於雙曲幾何的帖子中提到的,其中一個公設,即平行公設,與其他公設不同。
在托馬斯·希思對歐幾里得《幾何原本》的翻譯(也稱為我所擁有的譯本)中,五個公設被表述為
“設以下為公設
1)從任意點到任意點可以作直線。
2)有限直線可以沿直線無限延長。
3)以任意點為圓心,任意長為半徑,可作圓。
4)所有直角都彼此相等。
5)如果一條直線與兩條直線相交,且在同一側的內角之和小於兩個直角,則這兩條直線無限延長後,在內角和小於兩個直角的一側相交。”
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞事業 訂閱。透過購買訂閱,您正在幫助確保未來繼續有關於塑造我們當今世界的發現和思想的具有影響力的報道。
前四個簡短明瞭,但第五個卻很冗長。在圖片中更容易理解。
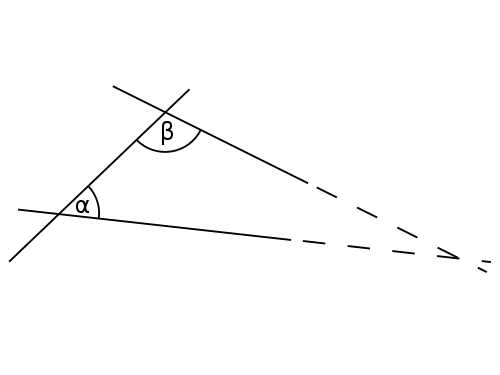
平行公設指出,如果角 α 和 β 的度數之和小於 180 度,則虛線最終會相交。圖片來源:6054,來自 Wikimedia Commons。CC BY-SA 3.0。
平行公設似乎很自然,但它是一種似乎應該是定理的陳述——我們可以使用其他公理和公設來證明的東西——而不是公設。 2000年來,數學家們試圖證明這一點,以表明平行公設可以從其他公理和公設中推匯出來。(關於試圖這樣做的數學家之一喬瓦尼·吉羅拉莫·薩切裡的精彩故事,請檢視託尼·克里斯蒂的部落格文章平行線的問題。)
每一次嘗試將平行公設作為定理證明的努力都註定要失敗,因為平行公設獨立於其他公理和公設。我們可以不使用平行公設,或者使用不同版本的公設來構建幾何,使其符合所有其他公理。雙曲幾何,我上一篇文章的主題,使用了不同版本的平行公設,因此最終得到了一個完全不同的幾何形狀。
我不是數學史學家,所以我對試圖證明平行公設的感受的想法是推測性的。但我將平行公設想象成床單上的皺紋,當你試圖撫平它時,它會移動,但永遠不會消失。人們試圖透過證明平行公設來“撫平”它,但他們只是將皺紋推到了其他陳述中。這些陳述對我來說很著迷。它們中的任何一個都可以取代平行公設,但與平行公設一樣,它們不能僅使用其他公設和公理來證明。
普萊費爾公理可能是與平行公設等價的最簡單的陳述。事實上,我學到它時就把它當作平行公設:在平面上,給定一條直線和一個不在該直線上的點,透過該點只能作一條與已知直線平行的直線。
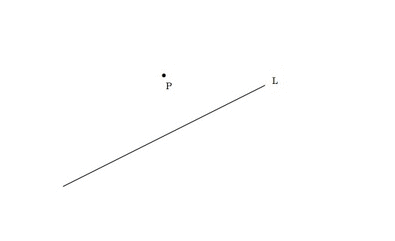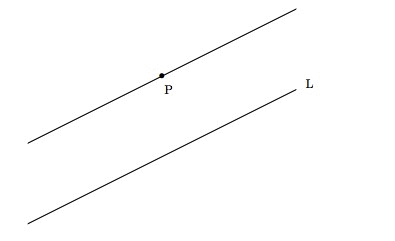
普萊費爾公理指出,透過點 P 只有一條直線不與直線 L 相交。圖片來源:伊芙琳·蘭姆。
普萊費爾公理簡單而直接,但一些與平行公設等價的最有趣的陳述涉及三角形。您可能還記得高中幾何課上三角形的角之和為 180 度。這隻有在您假設平行公設的情況下才成立。事實上,它等價於平行公設。但是等等,還有更多:所有三角形的角之和都相同的陳述也等價於平行公設。我認為這很吸引人,因為這意味著在其他幾何形狀中,存在內角和不同的三角形!例如,在雙曲幾何中,角之和可以是小於 180 度且大於或等於 0 度的任何數字。

這些雙曲三角形的角之和為 0 度。圖片來源:Saric,來自 Wikimedia Commons。
不難看出,不同幾何形狀中三角形的性質會導致其他形狀的性質。例如,歐幾里得幾何是唯一具有矩形的幾何形狀。為什麼?如果您透過繪製對角線將矩形分成兩個三角形,您最終會得到兩個全等三角形。矩形的角之和為 360 度,因此每個三角形的角之和必須為 180 度。如果您喜歡矩形,請堅持使用歐幾里得幾何。

如果您想再次看到這些,您最好接受平行公設。圖片來源:Webber,來自 Wikimedia Commons。
回到三角形,您可能還記得“相似”三角形和“全等”三角形的概念。如果兩個三角形具有相同的角,則它們是相似的;如果它們相似且具有相同的邊長,則它們是全等的。

相似但不全等的歐幾里得三角形。相似但不全等三角形的存在等價於平行公設。圖片來源:Nguyenthephuc,來自 Wikimedia Commons。
在歐幾里得幾何中,存在相似但不全等的三角形。事實上,有很多這樣的三角形。無論您從哪個三角形開始,您都可以將其放大或縮小到您想要的任何尺寸。然而,存在相似但不全等三角形這一事實非常特殊。這是又一個等價於平行公設的陳述!例如,在雙曲幾何中,三角形的角唯一地確定了其邊長。這有一個更令人驚訝的後果:歐幾里得幾何是唯一三角形可以任意大的幾何形狀。在雙曲幾何中,存在最大的三角形。
另一個關於三角形的且與平行公設等價的陳述是勾股定理:在直角三角形中,斜邊長度的平方等於另外兩條邊長度的平方和。它是我們在幾何學中學到的最早的定理之一,但只有在我們假設平行公設的情況下才成立。

奧利弗·伯恩 1847 年翻譯的歐幾里得《幾何原本》中的勾股定理插圖。勾股定理指出,黑色和紅色正方形的面積之和等於下方黃色和藍色正方形的面積。
正如亞歷山大·博戈莫爾尼在他的網站 Cut the Knot 上寫道,一些與平行公設等價的陳述似乎是顯而易見的,而另一些則完全不然:“無論如何,勾股定理遠非顯而易見。令人驚奇的是,平行公設與諸如[存在一對相似但不全等的三角形]和[三角形的面積沒有上限]等直觀陳述等價,並且也與勾股定理等價。”
由於幾個世紀以來,數學家們未能使用其他公設和公理證明平行公設,我設想他們一直在努力,試圖弄清楚如果他們假設平行公設為假會發生什麼。他們不斷努力,但他們永遠無法明確地找到矛盾之處。當他們不斷努力時,他們發現了這些陳述以及許多其他與平行公設等價的陳述。如果您假設其中任何一個,您最終都會得到歐幾里得幾何,但如果沒有它們,您可以找到通往非歐幾里得幾何的奇妙土地的道路,在那裡,角決定長度,並且沒有正方形!