本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
我上週進行了第一次期中考試。我正在為數學專業的學生教授一門大致初級課程,這是他們第一批主要側重於證明而不是計算或演算法的課程之一。它比他們到目前為止上的大多數數學課都更抽象。我喜歡教這門課,因為像這樣的課程讓我對數學感到興奮,所以它讓我想起了我生命中的一段特殊時光。
我的期中考試中的一個問題是:描述一個R2中的集合,它既不開也不閉。
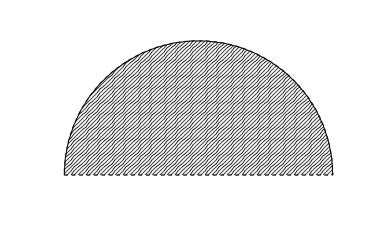
一個既不開也不閉的集合。半圓頂部的實線弧表示邊界的一部分包含在該集合中,而底部的虛線表示邊界的一部分不包含在該集合中。透過適當的標記和縮放,此集合可以描述為所有點 (x,y) 的集合,這些點距離點 (0,0) 小於或等於 1 個單位,並且 y 座標嚴格大於 0。來源:伊芙琳·蘭姆。
關於支援科學新聞事業
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞事業 訂閱。透過購買訂閱,您正在幫助確保有關塑造我們當今世界的發現和想法的具有影響力的故事的未來。
“開”和“閉”當然是術語。在我們的課堂上,如果集合中的每個點周圍都有一個小球也完全包含在該集合中,則該集合稱為“開”。如果我們只看實數軸,區間 (0,1)——所有嚴格大於 0 且嚴格小於 1 的數字的集合——是一個開集。如果您在區間 (0,1) 中選擇一個數字,無論它多麼接近端點之一,它周圍總有一個較小的區間也完全包含在區間 (0,1) 中。例如,數字 1/100 非常接近 0,但區間 (1/200, 1/50) 包含點 1/100 並且完全包含在區間 (0,1) 中。另一方面,區間 [0,1]——所有大於或等於 0 且小於或等於 1 的數字的集合——不是開集。[0,1] 和 (0,1) 之間的唯一區別是我們是否包含端點,但這兩個小點卻造成了很大的區別。點 0 周圍的每個區間都包含負數,因此點 0 周圍沒有完全在區間 [0,1] 中的小區間。因此,區間 [0,1] 不滿足開集的定義。(有關開集的更多資訊,請檢視維基百科或MathWorld。)
如果一個集合的補集是開集,則該集合稱為“閉集”。我們的課程幾乎完全在正常的歐幾里得空間中進行,而不是在一些更奇特的空間中。在 d 維歐幾里得空間 Rd 中,集合 A 的補集是 Rd 中但不在 A 中的所有內容。區間 [0,1] 是閉集,因為它的補集,即嚴格小於 0 或嚴格大於 1 的實數集合,是開集。
所以我的期中考試題要求學生找到一個既不開且補集也不開的集合。我以為這將是考試中最容易的問題之一,所以我很驚訝我的許多學生在這個問題上犯了同樣的錯誤。他們沒有給我既不開也不閉的集合,而是給了我既開又閉的集合!
我低估了英語語言的力量,它會向我的學生暗示數學上不正確的陳述。在數學中,“開”和“閉”不是反義詞。集合可以是開集、閉集、既開又閉,或者既不開也不閉。(既開又閉的集合有時稱為“開閉集”。)“閉”的定義包含一定程度的“相反性”,因為集合的補集有點像它的“相反”,但閉集和開集本身並不是相反的。如果一個集合不是開集,那並不會使其成為閉集,如果一個集合是閉集,那並不意味著它不能是開集。它們是相關的,但這不是互斥關係。但在英語中,這兩個詞基本上是反義詞(儘管對於門和蓋子,除了開和閉之外,我們還可以選擇“半開半閉”)。我的學生使用了他們對英語中“開”和“閉”這兩個詞如何相互關聯的直覺,並將這種直覺應用於這些術語的數學用法。
他們中的一些人甚至透過說“因為 [A] 是開集,所以它不是閉集,並且因為它不是閉集,所以它不是開集”之類的話來為他們的答案辯解。他們事實上知道存在一個既開又閉的集合,但他們並沒有完全理解它,所以他們不知何故得出了一個自相矛盾的結論,即既開又閉的集合既不開也不閉!
當然,除了語言之外,還有其他因素在起作用:時間可能是考試環境中的一個問題,考試的壓力有時會讓人寫出甚至他們自己後來都不明白的奇怪的東西。但我認為“開”和“閉”這兩個詞的數學含義和英語含義之間的差異在我的學生解答考試題時遇到了困難,這起到了很大的作用。我不認為他們會在披薩配料方面犯同樣的錯誤。這個披薩上既有乳酪又有義大利辣香腸。乳酪不是義大利辣香腸,義大利辣香腸也不是乳酪,所以這個披薩上有“非乳酪”和“非義大利辣香腸”,因此它既沒有乳酪也沒有義大利辣香腸。“義大利辣香腸”和“乳酪”在英語中不是像“閉”和“開”那樣的反義詞。
我的學生在這個問題上的錯誤對我來說很有價值,我希望對他們也是如此,儘管丟了分。我瞭解到我的學生仍在習慣“開”和“閉”的概念,這在課程的其餘部分以及更重要的是他們仍在習慣使用數學定義方面將繼續很重要。我認為數學家異常擅長接受新定義,忽略先前的知識,並僅使用該定義進行工作。我們探究定義的不同部分,並嘗試瞭解如果我們刪除或新增條款,它會有什麼不同。我們可以從定義中“自然而然地”獲得哪些定理?正如Cathy O'Neil 在這裡討論的那樣,建立好的定義是一門藝術,這在數學中非常重要。但我的學生是剛入門的數學家,他們尚未熟練掌握這門藝術。
有一個名為Math Mistakes的部落格,它收集了中小學生不正確的作業的有趣例子並對其進行分析。學生犯這些錯誤時在想什麼?解決他們的誤解的最佳方法是什麼?與普遍的看法相反,考試並非純粹是折磨人的工具或懲罰的手段。考試也可以是評估學生進步和診斷學生誤解的一種方式。我希望現在我已經診斷出我的課堂中對“開”和“閉”的常見誤解,我可以澄清它並嘗試避免將來出現類似的錯誤。