本文發表於《大眾科學》的前部落格網路,僅反映作者的觀點,不一定反映《大眾科學》的觀點
你如何判斷你的星球是什麼樣子的?一種方法是發展太空計劃,發射飛船,並從遠處拍攝它的照片。幾臺相機和極少數人類離開了地球,從太空觀察它,他們說它看起來像一個球體。但如果他們在撒謊呢?雖然最近的一篇論文表明,要維持一個由所有航天機構、宇航員和行星科學家組成的全球陰謀集團將是困難的,但我們不必相信他們的話。
除了發展太空計劃之外,還有一種數學上巧妙、實際上不可能的方式來確定我們居住的表面型別:尤拉示性數。(這是以萊昂哈德·尤拉命名的事物列表中的眾多條目之一。)早在太空計劃,甚至哥倫布存在之前,人類就知道地球是球體。這不是他們弄清楚的方式。
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道 訂閱。透過購買訂閱,您正在幫助確保未來能夠講述關於塑造我們今天世界的發現和想法的有影響力的故事。
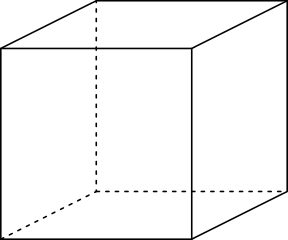
像年齡一樣,尤拉示性數只是一個數字。對於像盒子、沙灘球或行星這樣的二維表面,它是物體的頂點數減去邊數加上面數,即V-E+F。我們將從一個簡單的例子開始,一個立方體。一個立方體有8個頂點、12條邊和6個面,所以總共是8-12+6=2。
球體呢?在這裡,頂點和邊不是憑空出現的。我們必須畫出來。一種方法是在地球儀上畫一條赤道和一些經線。或者,如果你沒有地球儀,可以用橡皮筋繞一個葡萄柚。

我沒有球形相機,所以如果你沒有自己的葡萄柚,你只能相信我的話,那裡有6個橡皮筋相交的頂點,12條線段和8個三角形,尤拉示性數為6-12+8=2。(這些數字恰好與立方體的數字相似。你能弄清楚為什麼嗎?)
在進行計算時做出選擇總是很冒險的。我們對如何在葡萄柚上放橡皮筋做出了選擇。如果我們以不同的方式做呢?這次我在上面放了四根橡皮筋。

現在它有10個頂點,21條邊和13個面,再次得到,10-21+13=2。
事實上,無論我們如何透過繪製線條或在球體上放置橡皮筋來分解它,我們最終都會得到尤拉示性數2。* 你不必相信我的話。一個嚴謹的證明有點複雜,但你可以透過塗鴉輕鬆地讓自己信服。畫一個形狀,並在其中畫一些頂點和邊。新增一個頂點和一些邊。尤拉示性數會發生什麼變化?擦除一條邊。現在會發生什麼?
尤拉示性數是一個拓撲不變數,這意味著拉伸或擠壓物體不會改變它,只有撕裂或粘合才會改變它。因此,尤拉示性數可以用來確定表面的拓撲結構,但不能確定其更精細的特徵。例如,立方體、球體、四面體和其他像它們這樣的封閉形狀都具有相同的尤拉示性數,因為它們在拓撲上是等價的。
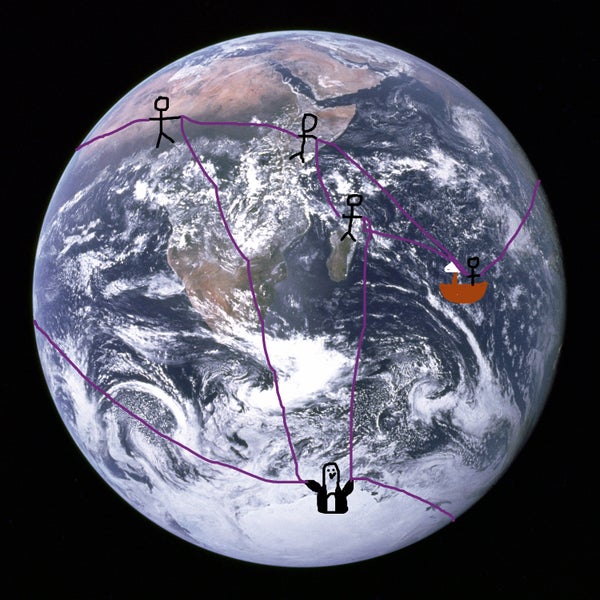
如果你是一個對科學好奇的人,沒有機會進入太空親眼看看地球,並且不想相信古代科學家或NASA的話,你可以使用尤拉示性數來確定這個星球的拓撲結構。你只需要幾個朋友和很多繩子。
每個人都站在地球上的一個點上,每個人都拿著幾根繩子的末端。現在你數一下有多少人,有多少段繩子,以及在這些繩段中封閉了多少個區域。然後求出尤拉示性數,V-E+F。
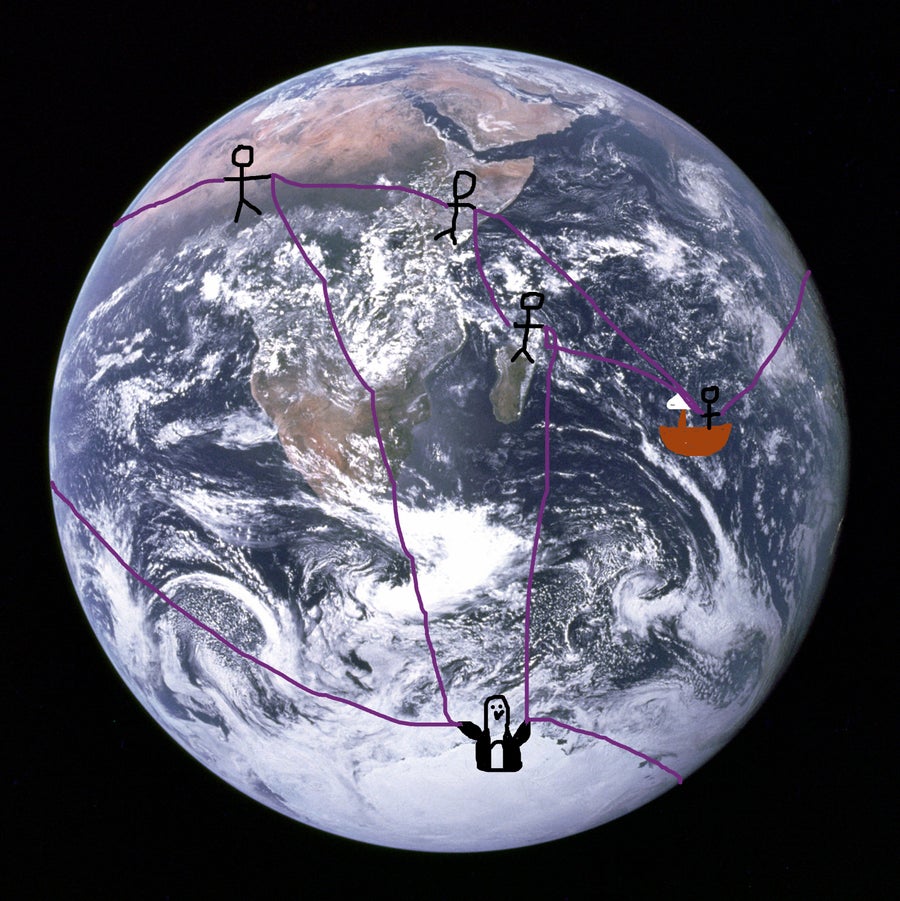
未按比例。
如果你得到2,你就完成了。拓撲學上,唯一尤拉示性數為2的表面是球體。
如果你沒有得到2,你可能數錯了。但假設你是在一個拓撲結構尚未確定的外星球上。該星球的其他幾個方面將幫助你準確確定它是什麼樣的表面。
首先,這個世界是有限的,還是會永遠延伸到深淵?如果世界是無限的,你就無法將其劃分為幾個部分並找到尤拉示性數,那麼你就倒黴了。我們假設所有的世界都是有限的。

莫比烏斯帶。圖片:David Benbennick,透過維基共享資源。
接下來,我們要處理可定向性。莫比烏斯帶是最著名的不可定向表面:如果你一直繞著它走,你最終會回到你開始的地方,但在紙的另一面。對於可定向表面,你知道有內部和外部;你永遠不會倒著走回你的起點。無論你的星球是否可定向,你都可以使用尤拉示性數來確定其拓撲結構。
最後,邊界。你認為有可能從世界的邊緣走出去嗎?如果是,有多少個獨立的邊緣?可能只有一個環繞外部的邊緣,也可能有更多。也許你有理由相信地球的形狀像一個墊圈或一個加厚的8字形。
尤拉示性數、可定向性和邊界部分的數量唯一地決定了你的星球是什麼樣的表面。如果你得到2,你肯定在一個球體上。增加一個邊界部分會使尤拉示性數減少1,所以如果你得到1,你是在一個被刺穿的球體上,它在拓撲學上等同於平面中的多邊形。如果你得到0,你可能住在一個環面上,或者你可能住在一個墊圈上。列表還在繼續。
一旦你知道你的星球在拓撲學上是什麼樣子的,你就可以開始弄清楚它的幾何形狀。如果你得到2,你可以嘗試找出你是否住在一個球體、立方體、足球或其他奇異表面上。尤拉示性數在這裡幫不了你。我建議你借鑑埃拉托色尼和其他古代天文學家的做法,開始使用陰影來確定地球在任何特定點的彎曲程度。伊桑·西格爾可以告訴你所有關於這方面的事情。
致謝:我第一次接觸到使用尤拉示性數確定你的星球拓撲結構的想法是在我的朋友猶他大學數學家凱文·沃特曼的一次演講中。B.o.B. 和尼爾·德格拉斯·泰森啟發了我完成這篇文章的寫作。
*為了回應評論,我要補充一點,你封閉的區域不能有孔。也就是說,它們應該像圓盤,而不是墊圈。技術術語是“單連通”。確保所有區域都是單連通的一種方法是三角剖分你的表面。