本文發表於《大眾科學》的前部落格網路,並反映了作者的觀點,不一定反映《大眾科學》的觀點。
您在智慧領域中跋涉。在遠處,您看到一絲閃光。難道是它嗎?是的,這就是您尋找的球體!在您探索完整個表面之前,您只需要再收集幾個了。
David Madore是一位法國數學家,他創造了這個以及其他在雙曲平面上玩的遊戲。Madore的迷宮是我發現的眾多有趣工具之一,可以幫助我直觀地瞭解雙曲幾何的工作原理。我推薦的其他工具包括戴娜·泰米娜的鉤針編織專案,它允許您建立可觸控的雙曲空間模型,以及馬林·克里斯特松的雙曲平鋪工具。
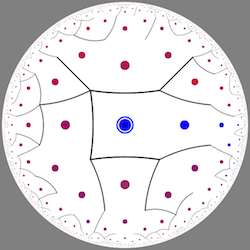
來自David Madore雙曲迷宮的靜幀。
關於支援科學新聞報道
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞報道: 訂閱。透過購買訂閱,您將幫助確保有關塑造我們當今世界的發現和思想的具有影響力的故事的未來。
Madore有三款遊戲可供選擇:“玩具”版和普通版的經典迷宮,以及尋求智慧、正義和其他美德之球的探險。所有三款遊戲都可以在雙曲平面的龐加萊圓盤模型或貝爾特拉米-克萊因模型上進行。雖然無論您是否關心幾何學,這些遊戲都很有趣,但它們也融入了一些關於雙曲面的複雜概念。
為了理解Madore迷宮的工作原理,我們將簡要地介紹一下標準的歐幾里得平面。如果我們從平面上的一個點走開,我們將離該點越來越遠。(這種說法並非完全是同義反復;如果假設我們生活在一個球面上,我們最終會開始再次靠近起點。)但是有一種方法可以將無限平面變成有限空間。這與環繞式影片遊戲(如小行星)的製作者使用的技術相同。
.png?w=300)
單孔環面可以剖析成正方形,雙孔環面可以剖析成八邊形,三孔環面可以剖析成十二邊形的示意圖。圖片來自艾倫·哈徹的教科書《代數拓撲學》。
您從一個正方形開始,並將相對的邊粘合在一起。當您走出正方形的一邊時,您會從另一邊進入。您可以將其表示為環面或甜甜圈,一個正方形,或平鋪著無限多個全等正方形的平面。當您穿過其中一個的邊時,您會走進下一個的相對邊。因為這些是表示相同場景的不同方式,所以歐幾里得平面上的路徑等同於環面上的路徑。
Madore的雙曲迷宮使用了相同的想法,只不過我們使用的是雙曲平面而不是歐幾里得平面中的正方形。如果我們從雙曲平面中的八邊形開始,我們可以將邊粘合在一起,得到一個有兩個孔而不是一個孔的甜甜圈。如果我們從十二邊形(十二條邊)開始,我們可以得到一個三孔環面。具有更高虧格的曲面也可以表示為雙曲平面中的多邊形,而這正是Madore在他的雙曲迷宮中所做的。每個迷宮都在雙曲平面上進行,但Madore使用的粘合意味著它等同於在具有很多孔洞的曲面上進行遊戲:玩具版有4個孔洞,完整版有8,812個孔洞。Madore在頁面底部提供了關於他用於建立遊戲的數學原理的更詳細解釋。
在您玩遊戲時,您可以留意雙曲空間的一些有趣方面。首先,您可以檢視雙曲平鋪如何隨著您的移動和棋盤重新居中而改變形狀。您還可以透過在兩種檢視之間切換來探索雙曲空間的龐加萊圓盤模型和貝爾特拉米-克萊因模型之間的差異。您更喜歡哪一個?
如果您更喜歡拓撲學而不是幾何學,您可以檢查曲面上的環。拓撲學中最重要的工具之一是同倫,即對空間中的環進行分類的過程。在平面上,任何兩個環在某種程度上都是等價的:您可以毫不費力地將一個環拖到另一個環上。另一種思考方式是,從一個指定點到另一個點的任何兩種行走方式在某種程度上都是相同的。然而,在環面上,並非所有環都是等價的。環繞環面孔洞的環與將您的拇指和食指穿過孔洞所得到的環是不同的。同樣,在具有更多孔洞的曲面上,有很多環是不相同的。Madore在迷宮中提出的挑戰之一是沿著基本不同的路徑來回走動。
您還可以使用Madore的迷宮來探索雙曲幾何的一個決定性特徵:直線彼此發散的事實。在探險遊戲中,您可以在移動時留下“麵包屑”。您偶爾會遇到過去的“麵包屑”,但您會發現,不知不覺中,您甚至再也看不到它們了,即使這些蹤跡有時非常接近。
您能想出找到所有球體的最佳策略嗎?是更好地徹底搜尋一個領域,還是隻是不斷向前走,來回穿梭於所有領域?找到所有球體需要多長時間?信不信由你,這些問題與遍歷理論和動力系統中的一些主題有關,許多數學家都在研究這些主題,包括菲爾茲獎得主阿圖爾·阿維拉、埃隆·林登施特勞斯和瑪麗安·米爾扎哈尼。
幾何學、拓撲學和動力學:對於一個易於操作的電腦遊戲來說還不錯。祝您探索愉快!