本文發表於《大眾科學》的前部落格網路,反映了作者的觀點,不一定反映《大眾科學》的觀點
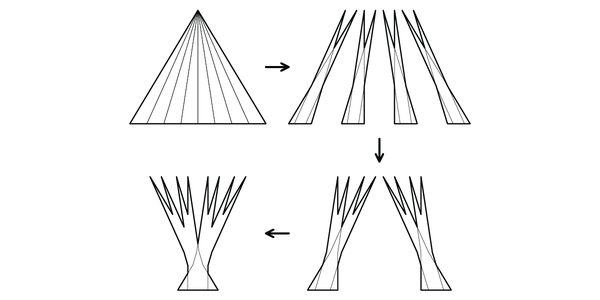
去年,我寫了關於卡克亞針問題的文章,這是一個數學小問題,當我擔心自己可能會陷入困境時,我會求助於它以尋求安慰。 該問題要求您在平面上旋轉細針所需的最小面積。下面是一個在平面上的小區域內旋轉針的例子。
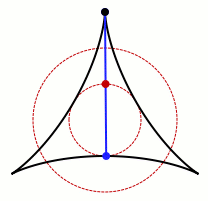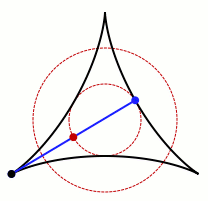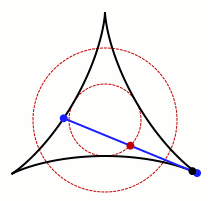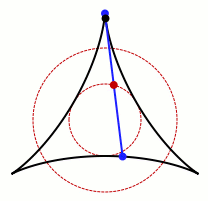
一個允許卡克亞的針旋轉的集合的動畫。 鳴謝:Claudio Rocchini Wikimedia (CC BY-SA 3.0)
令人驚訝的是,針可以在面積任意小的集合中旋轉。這個事實是 阿布拉姆·薩莫伊洛維奇·貝西科維奇 於 1928 年證明的。他的結果基於他之前關於平面上包含指向各個方向的單位長度線段的集合的研究。 為了紀念他,這些集合被稱為貝西科維奇集合。
關於支援科學新聞
如果您喜歡這篇文章,請考慮透過以下方式支援我們屢獲殊榮的新聞工作 訂閱。 透過購買訂閱,您正在幫助確保關於當今塑造我們世界的發現和想法的影響深遠的故事的未來。
貝西科維奇集合看起來真的很酷,所以我很高興在預印本伺服器 arxiv.org 上看到一篇關於 最小貝西科維奇排列 的論文。 但是,當我開始閱讀它時,我既失望又好奇。 該論文不是關於平面上的貝西科維奇集合,所以我沒有看到很多漂亮的圖片,但我瞭解了卡克亞針問題的另一個版本。 該論文研究了卡克亞針問題在不同數學環境中的轉換,即有限域和有限平面世界。
我們習慣於使用像實數這樣的無限數域進行算術運算,但我們也可以在有限的數字集合上定義基本運算。例如,在模算術中,也稱為時鐘算術,您有一個模數——比如 12——當您新增或乘以兩個數字時,您檢視除以模數時的餘數。當您想到 10:00 五小時後是 3:00 這個事即時,該系統似乎並不那麼陌生。 在報時時,我們習慣於使用模數為 12 或 24 的算術運算。(出於技術原因,對於卡克亞針問題的有限版本,模數需要是素數或素數的冪。沒有卡克亞時鐘!)
正如我們可以將二維平面視為所有實數對的集合一樣,我們可以考慮由有限集合的成員對組成的有限平面。 例如,如果模數為 2,則該域僅包含數字 0 和 1,並且該平面為數對 {(0,0),(0,1),(1,0),(1,1)}。我們也可以檢視這些數字的三元組,如果您閱讀《統一之根》一段時間了,您可能會記得一個名為範諾平面的空間。 (如果不是,您可以在這裡閱讀相關內容。)構建範諾平面的一種方法是從零和一的三元組而不是數對開始,因此在某些方面,它是有限域上平面的三維版本。 (在此處閱讀有關該描述的更多資訊。)
標準二維平面中的任意兩點都確定一條直線。在有限平面中也會發生同樣的事情。在有限平面中,“方向”的概念不像在標準二維平面中那麼清晰,但是研究過有限卡克亞針問題的人們將有限版本的貝西科維奇集合定義為平面中包含平面上每條直線上的點的集合。
為什麼要將卡克亞的針移動到像有限平面這樣陌生的空間呢? 除了對改變假設會發生什麼情況的數學好奇心之外,這個問題是由於一個叫做卡克亞猜想的東西引起的。雖然存在面積任意小的卡克亞集合,並且存在零面積的貝西科維奇集合(使用一種稱為勒貝格測度的標準面積測量方法),但該集合的維度仍然為 2。數學家已經推廣了維度的概念,以涵蓋維度不是整數的集合,有時我認為具有零測度是一種症狀,可能表明我們正在以“錯誤”的維度測量其面積。 但對於卡克亞來說,情況並非如此。 平面上的貝西科維奇集合實際上是二維的。 卡克亞猜想將這個想法推廣到更高的維度:在維度n 中,每個方向上都有單位長度線段的集合必須具有維度n,即使它在該維度中的測度為 0。
一些數學家開始研究有限平面版本,以此來研究微型的卡克亞猜想。 有限平面和無限平面有很多不同之處,但如果他們能夠在有限空間中取得一些進展或獲得一些直覺,他們可能會對更普遍的問題獲得一些見解。 有關卡克亞猜想的更多資訊,請參閱 Terry Tao 的這篇文章 或 Zeev Dvir 的這篇論文。
我認為有限卡克亞針問題是數學研究可以採取的曲折路徑的一個很好的例子。 我們從一個有趣的問題開始,該問題是出於對一些相當有形的事物自然的好奇心而產生的,將問題推廣到新的領域,發現那裡太難解決,然後將問題轉化為其他領域,目的是在那裡獲得一些進展。 激發該問題的最初想法被改變和模糊了,但數學家們希望新的、不同的問題可以幫助他們更好地理解整體情況。